Welkom in het 2e deel van de reeks kwantumcomputers & cryptografie. We gaan in op de huidige stand van zaken in kwantumcomputerland en schijnen licht op vragen zoals: “Hoe ver staan we met de bouw van kwantumcomputers?”, “Hoe moeilijk is het bouwen ervan?” en “Zullen ze binnen 10 jaar klassieke computers op vele fronten ingehaald hebben?” .
Quantum supremacy
Quantum computing wordt momenteel erg gehypet. Niet alleen liggen de verwachtingen erg hoog maar ook de terminologie is misleidend, meer bepaald de term quantum supremacy (kwantumsuperioriteit) die een veel zwakkere inhoud heeft dan wat de term op zich doet vermoeden. De term werd in 2012 voorgesteld door John Preskill. Het doel van quantum supremacy is aantonen dat een kwantumcomputer een probleem kan oplossen dat een klassieke computer in de praktijk niet kan, onafhankelijk van het nut van deze oefening. Het oplossen van exact één, in de praktijk nutteloos probleem, volstaat bijgevolg om quantum supremacy te bereiken. Het luidt dus allerminst het einde in van de klassieke computer. Preskill schreef in 2019 zelf dat de term niet ideaal is, niet alleen omdat het de hype versterkt, maar ook omwille van de sterke ideologische lading van het woord ‘supremacy’.
Google claimde eind 2019 in het natuurwetenschappelijk tijdschrift Nature quantum supremacy door middel van de Sycamore kwantumcomputer, die 53 werkende qubits bevatte. De claim had weliswaar betrekking op een in de praktijk nutteloos probleem, met name het genereren van willekeurige gekozen getallen volgens een zeer specifieke distributie die makkelijk is voor een kwantumcomputer maar moeilijk voor een klassieke computer, gezien die laatste daarvoor complexe simulaties moet doen. Hun kwantumcomputer kon dit in 200 seconden, daar waar een klassieke computer, aldus Google, 10 000 jaar nodig zou hebben.
IBM sprak de claim al snel tegen en stelde dat een klassieke computer dit, conservatief geschat, in 2,5 dagen zou kunnen en bovendien met een veel hogere nauwkeurigheid. Ook Koen Bertels, een Belgische professor aan de TU Delft en hoofd van het Quantum Computer Architectures Lab aan diezelfde universiteit, is duidelijk: “De recente claim van Google, waarbij ze beweerden dat hun kwantumcomputer een complexe berekening véél sneller kon uitvoeren dan de krachtigste supercomputers die we momenteel hebben, is simpelweg niet waar.” Ondanks de sterke prestatie van Google is hun claim van quantum supremacy betwistbaar. Toch is dit wellicht slechts een kwestie van tijd voor dit werkelijk het geval zal zijn.

Hoogstens – en ook dit is betwistbaar – is quantum advantage bereikt, waarmee bedoeld wordt dat een kwantumcomputer een – al dan niet nuttig – probleem sneller kan oplossen dan een traditionele computer. Reeds in 1994 werd daartoe het probleem van Simon bedacht, wat volstrekt nutteloos is, maar, net zoals het Sycamore experiment, op zo’n wijze geconstrueerd was om een kwantumcomputer een maximaal voordeel te geven ten opzichte van een klassieke computer. Tot op heden is quantum advantage hier nog niet aangetoond.
State of the art
Waar staan we vandaag? IBM claimt een kwantumcomputer met 53 qubits, Googles Sycamore heeft er 54 (waarvan eentje niet werkte tijdens hun fameuze experiment). Google claimde reeds in 2018 met hun Bristlecone een 72 qubit computer. Toch mag niet enkel gekeken worden naar het aantal qubits. Ruis en foutenmarges op verschillende vlakken, het niveau van verstrengeling tussen de qubits en de al dan niet ondersteunde kwantum logische poorten dragen allen bij aan de uiteindelijke kracht van de machine. IBM gebruikt daarom de term quantum volume om aan te geven hoe krachtig een kwantumcomputer werkelijk is. Helaas worden doorgaans maar weinig technische details prijsgegeven over kwantumcomputers.
Het bedrijf D-Wave verkoopt zogenoemde Adiabatische kwantumcomputers, waarbij hun krachtigste model 2048 qubits bevat. De kostprijs bedraagt zo’n 15 miljoen dollar. Midden 2020 wil D-Wave een kwantumcomputer met 5000 qubits op de markt brengen. Dat lijkt enorm vergeleken met die kwantumcomputers van IBM en Google. Het is echter gebaseerd op een ander paradigma uit de kwantummechanica – de Adiabatische stelling – waarbij veel minder verstrengeling vereist is. Testen door onder meer NASA, Google en ETH Zurich hebben niet kunnen aantonen dat de huidige generatie D-wave machines quantum advantage hebben, wat zoals eerder reeds aangegeven, betekent dat er een – al dan niet nuttig – probleem is waarvoor ze sneller zijn dan klassieke computers. Sommigen betwijfelen zelfs of dat ooit het geval zal zijn. De D-Wave machine werd in de markt gezet voor optimalisatievraagstukken en niet voor het kraken van moderne cryptografie. Toch zijn dergelijke kwantumcomputers in theorie equivalent met de universele kwantumcomputers, zoals die van Google en IBM. Weliswaar zal een D-Wave steeds meer qubits nodig hebben dan een even krachtige universele kwantumcomputer. Hoeveel meer hangt af van verschillende factoren en valt buiten het bestek van deze artikelenreeks.

Een kwantumcomputer bouwen
Het bouwen van een kwantumcomputer is enorm complex. Dit om verschillende redenen, waaronder isolatie, foutencorrectie en schaalbaarheid.
Laat ons eerst kijken naar de isolatie. Qubits zijn kleine deeltjes zoals elektronen (met spin) of fotonen (met een polarisatie). Die deeltjes zijn enorm gevoelig voor interferentie van buitenaf en moeten dus aan temperaturen dicht tegen het absolute nulpunt (-273,15° C) bewaard worden, afgeschermd van onder meer trillingen, licht en magnetische straling. Deze isolatie maakt het moeilijk om de qubits te controleren, te manipuleren en te lezen. Eén van de vele uitdagingen voor kwantumcomputers is het voldoende lang coherent houden ervan. De probabiliteiten – of correcter, de amplitudes – om 0 of 1 te meten kunnen immers verstoord worden alsook de verstrengeling tussen qubits. Men spreekt over de decoherence time om aan te geven hoe lang qubits in een coherente toestand blijven. In het geval van supergeleidende circuits, zoals in Googles Sycamore, situeert die decoherence time zich in de grootteorde van tienden of honderdsten van een microseconde. Er is de voorbij jaren veel vooruitgang geboekt om qubits beter af te schermen, maar desondanks zullen fouten allicht nooit helemaal vermeden kunnen worden. Hoogstens misschien ergens in de verre toekomst, voorbij onze huidige horizon. Radioactieve straling blijft bijvoorbeeld aanwezig, zelfs op het absolute nulpunt.
Daarom lijkt foutencorrectie noodzakelijk, waarbij meerdere fysieke qubits samen één logische qubit vormen. De fysieke qubits mogen tot op zekere hoogte fouten bevatten zonder dat het de waarde van de logische qubit die ze samen vormen impacteert. Die foutencorrectie is theoretisch mogelijk, hoewel het nog als onmogelijk beschouwd werd in de jaren ‘80 en ’90. Zo kunnen vijf fysieke qubits vereist zijn om één logische qubit te bekomen. Dit zal uiteraard stijgen indien de onderliggende qubits meer onderheving zijn aan fouten. Sowieso kan foutencorrectie enkel toegepast worden indien de qubits voldoende lange tijd in een coherente toestand blijven, wat op zich al een enorme uitdaging is.
Kwantumfoutencorrectie is een actief, maar vandaag wel een puur theoretisch onderzoeksdomein. We zitten zelfs nog niet in de fase van de experimenten. De huidige generatie kwantumcomputers maken er bijgevolg geen gebruik van (en kunnen dat ook niet). Toch lijkt het op termijn een noodzakelijkheid. Niettemin betwijfelen sommigen of foutencorrectie überhaupt wel in de praktijk mogelijk is. Eén van hen, niet de minste, is professor Fysica Mikhail Dyakonov aan de Université Montpellier. Eind 2018 schreef hij: “How many physical qubits would be required for each logical qubit? No one really knows, but estimates typically range from about 1,000 to 100,000.”
Dit brengt ons bij een andere uitdaging waar Dyakonov op ingaat: schaalbaarheid. De toestand van een traditionele computer met N bits wordt beschreven aan de hand van N bits. De toestand van een traditionele computer met 1000 bits wordt dus beschreven door 1000 bits, ofwel ongeveer 300 decimale cijfers. De toestand van een kwantumcomputer met N verstrengelde qubits wordt beschreven door 2N complexe getallen (ofwel 2N+1 reële getallen). Voor een kwantumcomputer met 1000 qubits betekent dit dus 21000 = 10300 complexe getallen.
Het werken met een kwantumcomputer houdt in dat de qubits, beschreven a.d.h.v. complexe getallen, gemanipuleerd worden met behulp van de kwantum logische poorten die op hun beurt beschreven worden aan de hand van – soms erg grote – matrices met complexe getallen (zie deel 1). Het is voor uw auteur vooralsnog onduidelijk hoe dit praktisch realiseerbaar zou kunnen zijn voor een kwantumcomputer met voldoende qubits om enigszins nuttig te zijn. Dyakanov: “A useful quantum computer needs to process a set of continuous parameters that is larger than the number of subatomic particles in the observable universe.” Vergeet niet dat de foutencorrectie van daarnet dit verder doet exploderen.
De complexiteit van kwantumcomputers stijgt dus exponentieel met het aantal qubits. Anders gezegd: één qubit erbij verdubbelt de complexiteit van de kwantumcomputer. Dit is anders bij klassieke computers. Daar stijgt de complexiteit lineair, wat betekent dat de complexiteit pas verdubbelt als ook het aantal bits verdubbelt.
Dit zijn maar drie van de uitdagingen. De huidige generatie kwantumcomputers op basis van supergeleidende circuits, zoals die van IBM en Google, hebben nog andere ernstige beperkingen. Bij een klassieke computer kun je bijvoorbeeld berekeningen doen op twee (of meer) waardes in het RAM geheugen, onafhankelijk van hun relatieve posities in het RAM geheugen. Ze hoeven dus niet aangrenzend te zijn. Kwantumcomputers op basis van supergeleidende circuits laten enkel operaties (door middel van poorten) toe op qubits die aan elkaar grenzen. Zoals onderstaande figuur toont, grenst een qubit in de Sycamore machine ten hoogste aan 4 andere qubits.
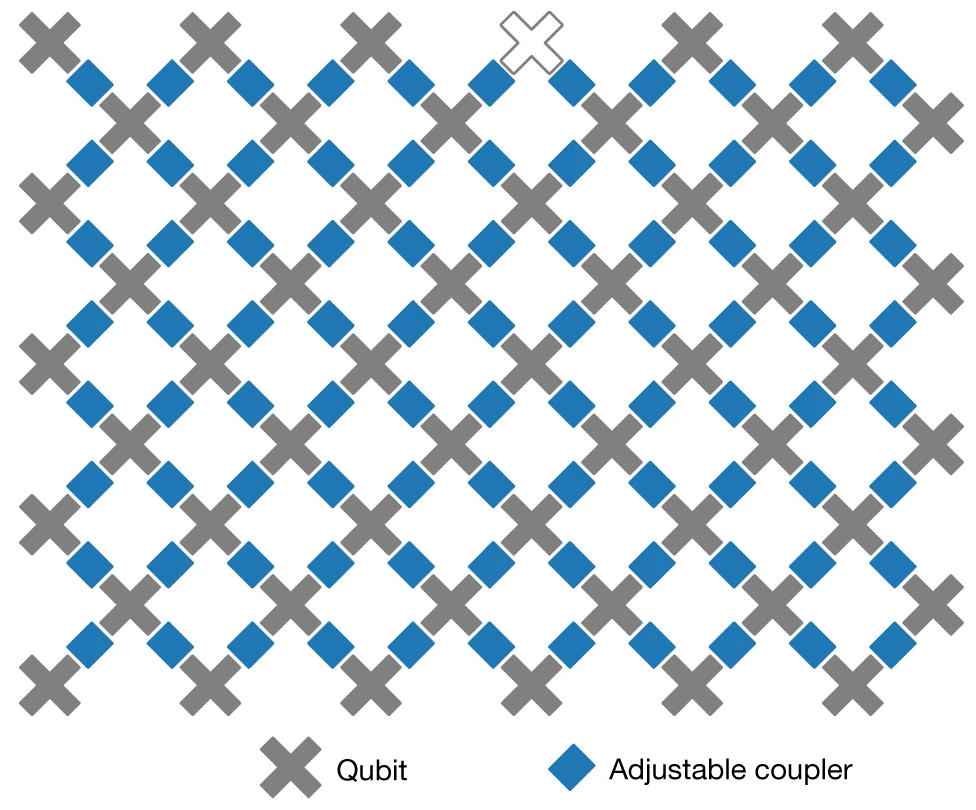
Volgt u nog? Samengevat zijn de uitdagingen enorm en lijken ze voor sommigen zelfs simpelweg onoverkomelijk. Sowieso is het interessant om te zien hoe de horizon van wat als mogelijk beschouwd wordt steeds opschuift. Foutencorrectie werd niet zo heel lang geleden zelfs puur theoretisch als onmogelijk beschouwd. Een nieuwe, inventieve benadering kan plots heel wat deuren doen opengaan. Toch is de realiteit vandaag dat de kwantumcomputer nog maar in zijn kinderschoenen staat en dat het enorme middelen zal vergen om die te ontgroeien.
Conclusie
Het idee van de kwantumcomputer dateert reeds van 1980 is daarmee ondertussen 40 jaar oud. Voorlopig zijn er experimenten door onder meer Google, IBM en Intel die getuigen van de enorme vooruitgang in het veld. Anderzijds zien we ook dat de luide claims toch wat in perspectief geplaatst dienen te worden en dat kwantumcomputers nog in hun kinderschoenen staan, al zijn er diverse beloftevolle initiatieven.
In de toekomst kijken is sowieso onmogelijk en er is dan ook niemand die met zekerheid kan zeggen of een nuttige kwantumcomputer ooit praktisch mogelijk zal zijn, laat staan wanneer. De meest optimistische schattingen gaan uit van vijf tot tien jaar, de meer voorzichtige plaatsen de horizon tussen 20 en 30 jaar in de toekomst. Ten slotte is er nog een minderheid die stelt dat het sowieso niet binnen afzienbare tijd zal zijn.
Een nuttige kwantumcomputer betekent overigens niet per se dat die ook onmiddellijk in staat zal zijn alle moderne cryptografie te breken. Wat exact de gevaren zijn van kwantumcomputers op de moderne cryptografie leest u binnenkort in het derde deel van onze vierdelige reeks kwantumcomputers en cryptografie.
Dit is een ingezonden bijdrage van Kristof Verslype, cryptograaf bij Smals Research. Het werd geschreven in eigen naam en neemt geen standpunt in namens Smals.

Een zeer verhelderend artikel! Dank daarvoor.