Mathématiquement parlant, un “réseau” est une structure composée de nœuds ou d’entités, ainsi que de relations entre ces nœuds (qu’on appelle souvent “arcs”). À l’origine, un “réseau social” est une “abstraction” d’une société : des personnes en constituent les nœuds et les liens entre ces personnes en sont les arcs (en fonction de ce qu’on veut étudier, il peut s’agir du fait de se connaitre, de travailler ensemble, d’être marié(e), d’être le père/la mère de …).
Un “réseau social” au sens plus commun du terme n’est rien d’autre qu’une interface informatique au-dessus de ce concept mathématique : sur Facebook, les nœuds sont les utilisateurs, et les liens les relations d’amitié (on parle de réseau non-dirigé : si A est ami avec B, B est également ami avec A) ; sur Twitter, les arcs sont les relations de “suiveur-suivi” (on a ici un réseau dirigé : A peut suivre B sans que B ne suive A en retour). On trouve par ailleurs des réseaux à d’autres niveaux : on peut établir des relations entre un ensemble de pages Facebook et les utilisateurs qui les “aiment” (font un “like”), ou entre des “posts” et les utilisateurs les ayant aimés ou commentés.
Dans cet article, nous allons voir comment on peut visualiser son propre réseau sur Facebook, et voir ce qu’on peut apprendre à la fois sur son réseau d’amis ou de connaissances, et sur ses amis eux-mêmes. La première chose à faire est d’extraire ses données depuis Facebook. Il existe plusieurs outils pour ce faire, tels que Netvizz ou NameGenWeb. C’est ce dernier que nous utilisons ici, avec lequel nous avons sélectionné tous les attributs possibles, et choisi le résultat au format “GraphML”. L’outil extrait la liste de tous ses amis “Facebook” en tant que nœud, et un arc est tiré entre deux amis dès qu’ils sont également amis entre eux. Remarquons que les amis de mes amis qui ne sont pas mes amis n’apparaissent pas dans le résultat. NameGenWeb propose également un outil de visualisation du réseau, mais nous avons préféré utiliser l’outil Gephi, logiciel open-source spécialisé dans la visualisation de graphes, dans lequel nous importons le résultat fourni par NameGenWeb (cet article n’est pas un tutoriel, nous n’allons volontairement pas rentrer dans les détails). On peut voir un graphe comme une représentation mathématique d’un réseau ; par abus de langage et pour ne pas compliquer les choses, en s’excusant auprès des puristes, nous ne ferons pas de différence entre “graphe” et “réseau” dans la suite de cet article.
 Comme on peut le voir ci-contre, l’importation dans Gephi ne semble pas très
Comme on peut le voir ci-contre, l’importation dans Gephi ne semble pas très
encourageante de prime abord. Les 566 nœuds de ce graphe sont disposés aléatoirement et reliés par 5133 arcs ! Pour mieux s’y retrouver, il faudra appliquer un algorithme de “layout”, de façon à mieux répartir les données dans l’espace. Gephi nous en propose une quinzaine. Nous sélectionnons “Force Atlas”, qui convient très bien pour ce type de graphe.
Le résultat est un petit peu meilleur, mais peu explicite. Nous allons maintenant lancer un algorithme de “modularisation”, permettant d’identifier les “clusters”, c’est-à-dire les groupes de nœuds particulièrement connectés, autrement dit 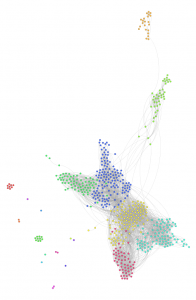 les groupes d’amis ayant beaucoup de connexions entre eux. Ceci se fera en cliquant sur le bouton “Run” à côté de “Modularity” (onglet “Statistics”), puis en coloriant le graphe dans l’onglet “Partition”, sur base de “Modularity Class”. Le résultat est visible sur l’image ci-contre (cliquer pour agrandir). Pour mieux comprendre ce que l’on voit, il conviendra de faire apparaître les labels (icône avec un T, je suggère par ailleurs de choisir “Hide non-selected” dans les options d’affichage).
les groupes d’amis ayant beaucoup de connexions entre eux. Ceci se fera en cliquant sur le bouton “Run” à côté de “Modularity” (onglet “Statistics”), puis en coloriant le graphe dans l’onglet “Partition”, sur base de “Modularity Class”. Le résultat est visible sur l’image ci-contre (cliquer pour agrandir). Pour mieux comprendre ce que l’on voit, il conviendra de faire apparaître les labels (icône avec un T, je suggère par ailleurs de choisir “Hide non-selected” dans les options d’affichage).
Remarquerons que le nœud “central”, c’est-à-dire la personne dont on a extrait le réseau, n’est volontairement pas présent dans le graphe. Si c’était le cas, il y aurait un arc entre ce nœud et chacun des autres nœuds du graphe.
Premières constations
En observant d’abord macroscopiquement, on voit apparaître des “grappes” de nœuds fortement connectés (c’est-à-dire un ensemble de personnes se connaissant mutuellement), certaines connectées au reste, d’autres totalement indépendantes. On trouve également quelques nœuds tout à fait isolés, correspondant à des amis “Facebook” ne connaissant (en tout cas sur Facebook) aucun autre de mes amis. Probablement des gens rencontrés à une occasion très ponctuelle, mais que l’on a perdus de vue depuis. On voit également apparaître tout en haut un groupe d’une vingtaine d’individus qui n’est connecté au reste que grâce à une personne. En regardant le résultat d’un peu plus près, il est frappant de voir à quel point les couleurs utilisées représentent en effet des groupes sociaux “de la vraie vie” : seront groupés par couleur, typiquement, les amis de l’école, de l’université, de la famille, ou de tel ou tel loisir. Des gens partageant donc quelque chose en commun : des études, un hobby, une famille, une ville d’origine, peut-être des convictions politiques ou religieuses, …
Nous pouvons également voir que la plus grande composante du réseau reprend 95% des nœuds (outil statistique “Connected Components”). Ce qui veut dire chaque personne parmi ces 95% est amie avec un de mes amis, qui est ami avec un autre de mes amis, …, qui est ami avec toute autre personne de cette composante. Le plus long chemin a une longueur de 12 sauts (mesure “Eccentricity” de l’outil statistique “Avg. Path Length”), ce qui veut dire qu’il faut 11 de mes amis pour connecter les deux amis les plus “extrêmes” de mon réseau. Notons que ça ne remet en rien en cause la théorie des six degrés de séparation, qui veut que chaque personne sur terre est connectée à chaque autre par une “chaîne d’amitié” composée de maximum six sauts, puisque rien ne dit qu’il n’existe pas un autre chemin plus court reliant mes deux amis “extrêmes”, mais composé de personnes avec lesquelles je ne suis pas ami.
Identifier les amis proches ?
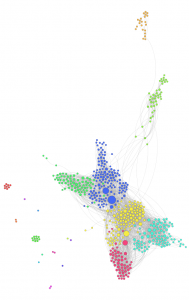 Dans pas mal de cas, il est possible d’identifier des amis “proches” (bien que ça soit difficile à définir formellement). Dans le domaine de la théorie des graphes, on parle de “centralité”. Il existe plusieurs façons de mesurer cette centralité : une de ces mesures est la centralité de degré, qui mesure le nombre d’arcs arrivant à un nœud. Un nœud à grande centralité de degré dans mon réseau Facebook que nous analysons ici signifie une personne avec laquelle j’ai un grand nombre d’amis communs (sur Facebook).
Dans pas mal de cas, il est possible d’identifier des amis “proches” (bien que ça soit difficile à définir formellement). Dans le domaine de la théorie des graphes, on parle de “centralité”. Il existe plusieurs façons de mesurer cette centralité : une de ces mesures est la centralité de degré, qui mesure le nombre d’arcs arrivant à un nœud. Un nœud à grande centralité de degré dans mon réseau Facebook que nous analysons ici signifie une personne avec laquelle j’ai un grand nombre d’amis communs (sur Facebook).
On peut visualiser ses amis proches en se servant du “ranking” (sélectionner le petit diamant, puis “Degree”), qui va faire apparaître en grand une personne avec laquelle j’ai beaucoup d’amis communs. En l’occurrence, ceux avec la plus haute centralité de degré sont mon frère, ma sœur, un ami très proche, puis un cousin avec lequel j’ai une activité commune (qui connait donc à la fois une grande partie de ma famille et des participants à la dite activité).
Des amis communs inattendus ?
Gephi va également nous permettre d’identifier des amis au sein d’un groupe social, également en lien avec des personnes d’un autre groupe. Il s’agit typiquement d’un collègue qui connait également un cousin, ou d’un camarade de classe en lien avec un ami de vacances. On va pour ce faire se servir d’une autre définition de la centralité : la centralité d’intermédiarité (betweeness centrality). Pour effectuer cette mesure, Gephi calculera le plus court chemin entre chaque paire de nœuds. Un nœud ayant une grande centralité d’intermédiarité sera sur un grand nombre de plus courts chemins. En général, cela veut dire qu’il sera connecté à plusieurs groupes distincts. Dans Gephi, on obtiendra cette centralité en lançant l’outil de statistique “Avg. Path Length”. Ensuite, on appliquera le “ranking” correspondant. En affichant la liste, on verra certainement apparaître tout en haut les mêmes noms qu’avec la centralité de degré, mais très vite apparaîtront des noms surprenants, qui ne sont pas spécialement proches. En regardant de plus près, on verra qu’effectivement, parmi les amis communs que l’on a avec cette personne, l’un ou l’autre sort du lot.
Et dans de mauvaises mains ?
Supposons que le graphe que nous avons construit ci-dessus tombe dans de “mauvaises mains” ; pourrait-il déduire à mon propos des informations que j’ai choisi de ne pas publier ? Pourra-t-il deviner à quoi correspondent les différents groupes de mon réseau ? L’idée est la suivante : supposons que je puisse déterminer que, parmi les 200 amis d’un certain Albert, 20 pratiquent le fitness (par exemple parce qu’ils sont publiquement membres d’un groupe autour du fitness, ou plus simplement l’affichent explicitement sur leur profil). Tel quel, ça ne me donne pas beaucoup d’information sur Albert. Il se pourrait que 10 % des gens en général pratiquent le fitness (cette affirmation purement arbitraire, sans aucun fondement statistique, n’est qu’un exemple illustratif !), il n’est donc pas étonnant de retrouver cette proportion dans les amis d’Albert. Par contre, si, grâce aux techniques mentionnées ci-dessus, j’identifie une “partition” de 30 personnes, particulièrement bien connectées, et dont Albert fait partie, et que parmi ces gens-là, j’en identifie 20 affichant leur intérêt pour ce sport, il y a beaucoup de chances qu’il s’agisse d’un groupe d’adeptes du fitness, qui se connaissent probablement grâce à leur pratique. Je pourrai donc en déduire qu’il est “probable” (nous ne rentrerons pas dans des calculs de statistiques et probabilités) qu’Albert pratique également ce sport.
En analysant ainsi les différentes partitions du réseau d’Albert, je pourrai sans doute dans certains cas identifier, par exemple, une école fréquentée par la majorité des gens d’une partition, une université … et donc déduire pas mal de choses sur ma “victime”.
En pratique ?
Sur le réseau extrait de mon profil, j’ai voulu dans un premier temps voir si l’on pouvait identifier celui correspondant à ma famille. L’idée étant que dans cette partition, il y a beaucoup de chance de trouver un plus grand nombre de personnes portant le même nom de famille. Et ça marche ! La proportion de personnes portant un des 3 noms de famille les plus fréquents de la partition est de très loin plus importante que dans toutes les autres partitions. Le même constat a pu être fait sur d’autres réseaux.
Nous avons aussi examiné la section “à propos” de chacun des profils de mon réseau, en ne considérant que ceux accessibles publiquement. Nous nous sommes intéressés de plus près à quatre partitions : une correspond à l’école où j’ai effectué toute ma scolarité, l’autre mes études supérieures, et deux autres à des activités qui ne sont pas référencées dans la section “à propos”.
Dans chacun de ces quatre réseaux, entre 40 et 50% des profils ont une section “à propos” publique. Le tableau ci-dessous reprend la proportion des partitions reprenant soit le nom de mon école secondaire, soit celui de mon université.
Sur l’ensemble de mes amis, les deux noms apparaissant pour chacun dans 12% de la section “à propos” de mes amis. Cette proportion est cependant nettement plus basse pour une grande partie des partitions (les 1 et 4 du tableau ci-dessous, mais toutes les autres avaient le même genre de valeur). Par contre, on trouve une partition dans laquelle 53% de personnes publiant leur parcours mentionnent le nom de mon école secondaire, et une partition avec 57% de référence à mon université, soit des proportions largement supérieures à toutes les autres partitions. Il n’y aurait donc aucune difficulté à déduire mon parcours d’enseignement rien qu’en observant mon réseau.
| [école secondaire] | [Université] | |
|---|---|---|
| tOTAL | 12 % | 12 % |
| Partition 1 | 4 % | 3 % |
| Partition 2 | 53 % | 25% |
| Partition 3 | 0 % | 57 % |
| Partition 4 | 8 % | 5 % |
La même chose a pu être faite en se basant sur les groupes : la requête de Graph Search “XXX’s groups” (voir notre article précédent) liste tous les groupes Facebook auquel une personne appartient. Cette information est publique pour chaque utilisateur (sauf pour les groupes “secrets”). Dans mon cas, je retrouve le nom d’une organisation dont je fais partie dans au moins un nom de groupe de 13% de mes amis. Mais, alors que ce nombre descend à 0 ou 1% pour la plupart de mes partitions, il monte à 29, 36 et 50% pour trois d’entre elles, qui correspondent effectivement à mes contacts au sein de cette organisation.
L’accès aux “likes” étant également largement public, le même genre de travail peut être fait à partir des likes de chacun des amis de quelqu’un.
Et alors ?
On pourrait se dire que ça n’est en rien problématique : il ne s’agit pas là d’informations très sensibles. Mais on pourrait aller plus loin : certaines personnes, certes peu nombreuses, affichent explicitement leur orientation religieuse. D’autres ne le font pas explicitement, mais une analyse rapide de leur profil permet de le deviner : pages liées à l’église ou à un Imam influent “likées”, commentaires ou photos au contenu à connotation explicitement religieuse, … une analyse, certes très laborieuses, des différentes partitions du réseau d’une “cible” pourrait permettre de deviner sa religion, même si elle ne donne aucune information à ce propos sur son profil. Et il en va de même pour les préférences politiques, ou l’orientation sexuelle. Il est bien évident que dans une démocratie digne de ce nom, il n’y a pas grand-chose à en craindre. Mais c’est sans doute moins le cas dans des pays où la liberté d’expression est plus que contrainte. Sans parler d’un malfrat qui voudrait mieux connaître la famille de sa cible avant de commettre un méfait. Il n’y a pas beaucoup de doute sur le fait que certaines polices ou autres services de renseignement se servent de ce genre de méthodes pour mieux cibler un suspect.
Par ailleurs, beaucoup de tentatives de piratage de type “phishing” ou “hameçonnage” à l’heure actuelle sont anonymes. Mais le jour où un courriel incitant quelqu’un à installer un logiciel ou à se connecter sur une copie de Facebook commencera par “Bonjour XXX [votre nom] ; ce week-end j’ai discuté avec YYY [un ami avec une haute centralité de degré] et ZZZ [un autre ami ayant beaucoup d’amis en commun avec YYY] à la fête de AAA [grâce aux photos ou évènements publiées par YYY ou ZZZ, voir notre article précédent], qui m’ont dit que tu serais intéressé par …”, il y a de fortes chances pour que les gens se méfient beaucoup moins. De façon générale, les techniques d’ingénierie sociale (voir l’article de Tania Martin à ce sujet) ont beaucoup de nouvelles perspectives à explorer.
Un document de la police fédérale belge consacré au vol d’identité écrit que l’intérêt pour des criminels “d’avoir accès aux réseaux sociaux est double : c’est d’abord d’avoir une connaissance de la hiérarchie ou des structures de réseaux d’amis des personnes concernées, et ensuite de dérober des renseignements classiques personnels via la technique du phishing”.
Mais, me direz-vous, encore faut-il que des gens mal intentionnés aient accès à cette information ; or, pour pouvoir télécharger le réseau que nous avons étudié dans cet article, il faut se connecter avec le compte que l’on veut analyser. Malheureusement, nous verrons dans notre prochain article qu’il n’est pas difficile de reconstruire la grande majorité du réseau d’amis de quelqu’un, même si celui-ci a configuré son profil Facebook pour que personne n’ait accès à sa liste d’amis. La suite au prochain numéro …

Pingback: Comment Facebook sait où vous allez, en vrai comme sur le net | Smals Research
Pingback: Facebook : peut-on vraiment cacher sa liste d’amis ? | Smals Research