Des données, à partir du moment où elles vivent et sont alimentées, souffrent presque systématiquement de problèmes de qualité. Le domaine de la Qualité des données (Data Quality) est vaste, très actif tant dans le monde académique qu’industriel. Il y a bien évidemment des aspects méthodologiques (améliorer les processus pour que les données qui rentrent soient les plus “propres” possible), mais également des aspects curatifs, pour nettoyer des données déjà collectées. On y trouve de nombreux aspects, tels que le dédoublonnage (matching, détection de doublons au sein d’une base de données), le couplage (entity linking, permettant de lier un enregistrement d’une base de données à un enregistrement dans un autre), mais également la “standardisation”, étape fondamentale sans laquelle les deux précédentes ne pourraient pas s’exécuter. Il s’agit de faire en sorte qu’une même chose soit toujours représentée de la même façon. Par exemple, que l’on n’ait pas d’un côté “Avenue Fonsny 20, 1060 Saint-Gilles” d’un côté, et “20 AV. FONSNY, 1060 BRUXELLES” de l’autre. Ou “02/787 57 11” pour l’un, “+3227875711” pour un deuxième, et encore “Tél: +32 (0)2 787 57 11” pour un troisième.

Il existe de nombreux outils et méthodes pour effectuer cette standardisation. Nous n’allons pas rentrer dans les détails de ces techniques ici. Mais il y a deux choses que tous les spécialistes de la “Data Quality”, qui viennent souvent en appui du “business”, mais ne sont que rarement au cœur du métier, s’accordent à dire :

1. Il n’est pas facile de convaincre le client que les données analysées souffrent d’un problème sérieux de qualité, et qu’il faut s’y attaquer. On peut bien sûr lister quelques exemples, mais ça ne suffit pas à illustrer l’ampleur du problème ;
2. Une fois les données traitées, il n’est pas non plus facile de montrer au client l’ampleur du gain, surtout si le client n’a pas établi d’indicateurs de qualité clairs. On peut compter les nombres d’enregistrement qui ont été modifiés par la standardisation (et les étapes qui ont suivi), mais ça ne suffit pas : mettre toute une colonne en majuscule peut affecter tous les records, mais le gain réel peut être très faible.

Valeurs à grande redondance

Dans un cas particulier, auquel nous avons été régulièrement confrontés, nous avons tenté de visualiser à la fois la situation de départ, ainsi que le gain obtenu après correction. Il s’agit de cas dans lesquels, dans une colonne ou un champ particulier, on s’attend à avoir relativement peu de valeurs rares. On a donc une grande redondance, la plupart des valeurs apparaissent de nombreuses fois. Supposons par exemple qu’une société ait un million de clients à travers le monde, pour chacun desquels elle possède une adresse. Le champ “Pays” sera probablement largement peuplé de valeurs présentes de multiples fois. Ou le champ “Ville” d’un grand nombre d’adresses dans un pays particulier. Ou la marque d’un grand nombre voitures présentes dans une base de données. Ou encore, comme illustré ci-dessous, le nom de la rue d’une liste comprenant les adresses de la totalité des entreprises présentes dans une ville en particulier.

Dans ces cas, une valeur unique ou rare (en regard du nombre total de lignes) sera souvent signe d’un problème de standardisation (“BRUXELLES” à la place de “Bruxelles”), d’une faute de frappe (“Bruxelle”) ou d’un enregistrement qui n’a rien à y faire (“Paris” pour un listing d’entreprises en Belgique). Mais trouver de tels exemples ne suffira pas à convaincre un client de s’atteler au problème. Il faut pouvoir le quantifier de façon plus tangible.

Prenons un exemple concret. Supposons que l’on ait une base de 500 lignes (disponible ci-joint), comprenant une colonne “Pays”, dont le nombre d’occurrences (par ligne et cumulées) de chacune des valeurs est reprise dans la table ci-contre.

Id	Pays	# Occur.	Somme cumul.
1	Belgique	100	100
2	France	90	190
3	Pays-Bas	90	280
4	Luxembourg	80	360
5	Allemagne	70	430
6	Italie	60	490
7	belgique	4	494
8	france	2	496
9	Beglique	1	497
10	italie	1	498
11	Fracne	1	499
12	pays-Bas	1	500

Distribution cumulée

La représentation visuelle de ce tableau synthétique, ci-dessous, se lit de la façon suivante : l’abscisse (axe horizontal) représente le nombre de valeurs distinctes, triées par nombre d’occurrences ; l’ordonnée (axe verticale) le nombre de records cumulés. Par exemple, on y voit que les 6 valeurs les plus fréquentes, soit 50 % des valeurs distinctes (d’où le “Median X” en label), représentent à elles-seules 490 lignes, soit 98 % des données.

Les valeurs uniques, elles (label “1’s”), représente un quart des valeurs (de 75 % à 100 %), mais seulement 0.6 % des données (de 99.40 à 100 %).

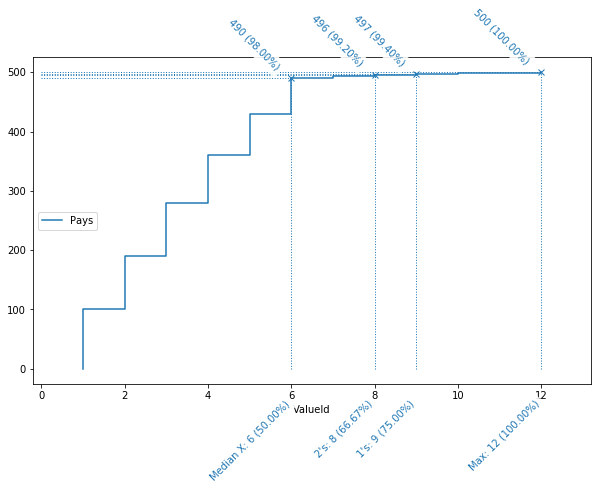
Ce graphique doit bien sûr être analysé en fonction du contexte, et il est difficile de tracer une courbe “idéale”. Mais dans le cas qui nous occupe, il est clair que cette courbe indique un problème sous-jacent. La partie droite de la courbe, avec une pente très faible, nous montre que les valeurs les plus rares ne représentent qu’une infime partie des données. La moitié des valeurs les moins présentes, ne représentent que 2 % des données. Si, pour des raisons “métier”, il y a peu de chances que des pays soient réellement aussi peu présents dans les données, on peut en déduire que la moitié des valeurs souffrent de problèmes de qualité.

Imaginons maintenant qu’avec un outil adapté, nous corrigions ces données. Le même exercice, sur base de données corrigées, pourra être repris sur le même schéma, représenté ci-dessous.

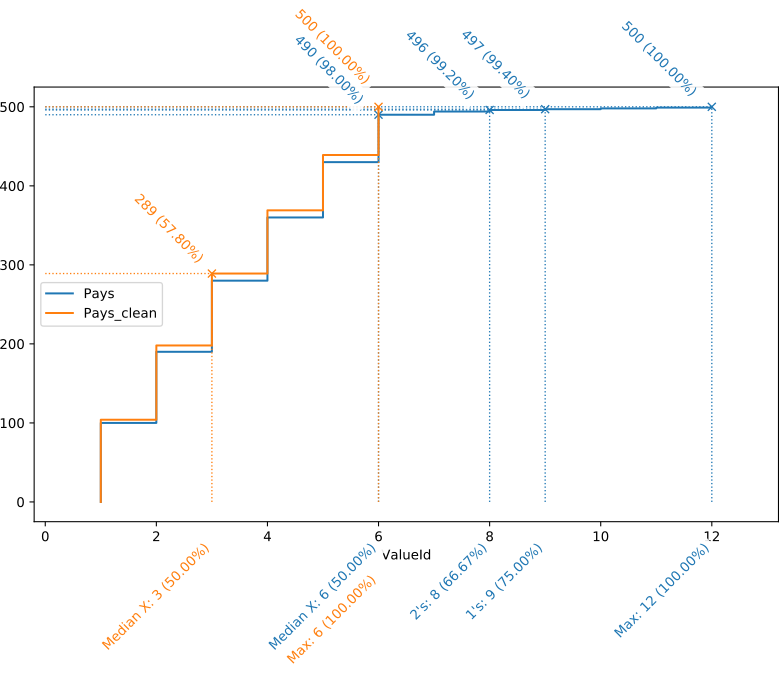
On peut remarquer dans la courbe orange, représentant la distribution des valeurs nettoyées, deux choses notables :

• Elle s’arrête moitié plus tôt que la bleue, signe qu’il n’aura fallu que la moitié des valeurs pour représenter la totalité des données ;
• Pour la partie en commun, les deux courbes sont à peine distinguables. La correction de “Beglique” (une seule occurrence) vers “Belgique” (100 occurrences) a en effet un impact non négligeable sur l’axe des valeurs (1/12è des valeurs), mais presque imperceptible sur l’axe des records : il fait passer “Belgique” de 100 à 101 occurrences.

Exemple réel

Considérons un exemple un plus réel. Nous partons pour ce faire des données disponibles en Open Data auprès de Banque Carrefour des Entreprises de Belgique (https://kbopub.economie.fgov.be/kbo-open-data), qui répertorie toutes les adresses des entreprises de Belgique. Nous en avons extrait, sur base du code postal, l’ensemble des adresses localisées dans la capitale, ce qui nous donne 266 446 adresses, pour lesquelles on trouve, en théorie, des champs distincts pour la rue, le numéro de maison, le code postal et la localité. Nous avons ensuite utilisé l’outil Open Source “OpenRefine” pour nettoyer celles-ci, en deux grandes étapes :

1. Une série d’opérations “batch”, appliquées sur chaque ligne sans tenir compte des autres, telles que :
   • Uniformisation de la casse, suppression des espaces superflus…
   • Détection et correction d’adresses mal découpées, typiquement avec un numéro de maison dans le champ “Street”
   • Correction des abréviations de type “Av”, “Blvd”, “Chée”…
2. Une série d’opération de “clustering”, qui consistent à identifier des valeurs qui se ressemblent (“Avenue Fonsny”, et “Avenue Fonsni”), et à remplacer, sous contrôle humain, toutes les valeurs d’un cluster par une même valeur, souvent la valeur majoritaire.

Dans le schéma ci-dessous, le champ de base est nommé “Street”, la version corrigée par les premières étapes “Street_batch”, et la version finale “Street_cluster”.

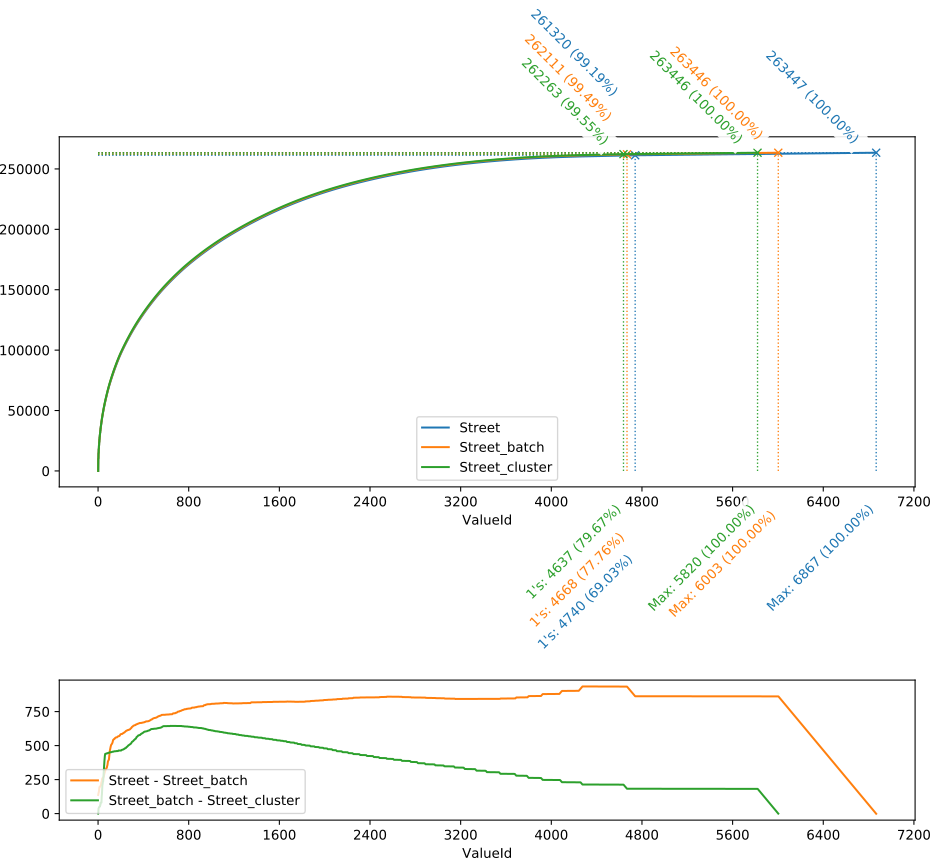
On peut observer de la figure ci-dessus (partie haute) que la principale différence entre les trois courbes se situe à l’extrémité droite, en particulier au niveau des valeurs uniques : entre la courbe bleue (données initiales) et la verte (après clustering), le nombre de valeurs uniques (à savoir la différence horizontale entre les “1’s” et les “Max”) a presque été divisé par deux (de 6867 – 4740 = 2127 à 5820 – 4637 = 1183) . Par contre, tout ce qui précède les valeurs uniques semble se confondre.

Pour mieux percevoir les différences entre les courbes, le graphique juste en dessous indique la différence verticale entre les courbes “Street” et “Street_batch” (orange), et “Street_batch” et “Street_cluster” (vert). Si cette courbe de différence est plate, horizontale, les deux courbes comparées croissent parallèlement. Ces deux courbes représentant des valeurs cumulées, leur croissante parallèle indique que les valeurs elles-mêmes, dans la zone plate, sont identiques ou similaires (ou à tout le moins que les variations s’annulent sur des courtes périodes).

Si, au contraire, cette courbe de différence croit, cela indique que, dans cette zone-là, les valeurs reçoivent plus d’occurrences dans la liste comparée que dans celle de base.

On peut donc en conclure, du graphique ci-dessus que :

• Avec la première série d’opérations (courbe orange), l’essentiel des changements ont eu lieu entre les valeurs uniques et les plus grosses valeurs, tout à gauche de la courbe. La majeure partie de la courbe étant approximativement plate, les autres valeurs (ni très fréquentes, ni très rares) ont été relativement peu impactées
• La seconde partie des opérations (clustering, en vert) a eu pour effet un transfert de valeurs de tout type (la grande majorité de la courbe étant en légère pente descendante) vers les valeurs les plus présentes (forte croissante du début de la courbe).

Il est aussi intéressant de constater que les valeurs uniques (mais on pourrait généraliser en parlant des valeurs “rares”, présentes par exemple moins que 3 ou 4 fois) représentent 20.33 % des valeurs distinctes (de 79.67 % à 100 %), mais 0.45 % des données (100 – 99.55). Un effort raisonnable a été nécessaire pour faire passer les valeurs uniques de 2127 à 1183. En regardant manuellement un échantillon de valeurs uniques restantes, il est facile de constater que la majorité des valeurs restantes sont incorrectes, et n’ont pas été corrigées par les opérations présentées ci-dessus. Suivant le principe de Pareto (qui, adapté à notre cas, stipule qu’il faut 20 % de l’effort pour corriger 80 % des problèmes, et 80 % de l’effort pour corriger les 20 % restant), il est probable que l’effort pour réduire plus fortement ces erreurs sera nettement plus conséquent, pour un gain relativement négligeable (seules 0.45 % des données sont concernées).

Un autre exemple

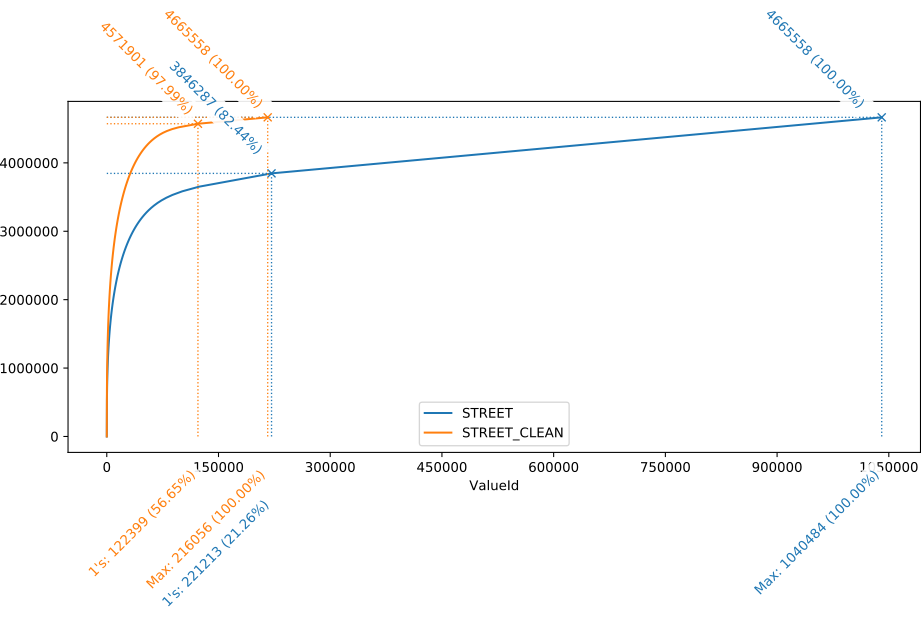
Le fait que les deux différentes courbes soient à ceux point peu distinguables dans l’exemple ci-dessus est principalement du au fait que le nombre de records correspondant à une valeur unique est au final relativement marginal : seulement 0.81% des données dans les données de base (champ “Street”). Nous avons été également confronté à des situations dans lesquelles le nombre de valeurs uniques était largement plus élevé. Le graphique ci-dessous reprend cet exemple (le champ “Street” d’une liste de 4.6 millions d’adresses), où les valeurs uniques représentent +/- 18 % des données (et près de 80 % des valeurs). Après nettoyage par un outil de Data Quality commercial, le nombre de valeurs uniques a été divisé par 8.7, le nombre de valeurs avec 5 occurrences ou moins par 6.8. Les données nettoyées ne contenait plus que 2 % de valeurs uniques. Avec une telle amélioration, la distinction entre les courbes est largement plus visible.

Pour conclure

Cette méthode est un premier pas permettant d’avoir un aperçu général de la distribution globale de la valeur d’un champ dans lequel on s’attend à une grande redondance, sans avoir à plonger dans les données proprement dites. Elle ne s’applique pas dans des situations où les valeurs sont plus uniques (numéros de téléphone, montant de commandes, identifiants…), et se concentre sur un champ à la fois. Il sera possible dans certains cas d’évaluer l’incohérence entre des champs (ville par rapport au code postal, par exemple) en concaténant plusieurs valeurs dans un seul champ (une combinaison incorrecte ayant peu de chances d’être fréquente).

La méthode présentée permettra d’évaluer une situation initiale, d’estimer l’impact que pourra avoir un effort de standardisation, et de comparer les données initiales avec les données traitées.

Dans un prochain article, nous présenterons une méthode complémentaire à celle-ci, dans laquelle on évalue le taux de similarité des valeurs entre elles : “Rue Fonsny” est très similaire à “Rue fonsny” et “Rue Fonsny 20”. Nous verrons que souvent, un taux de similarité interne important dans une liste sera un signe de problèmes de qualité.

Le code source (notebook Jupyter) nécessaire à la réalisation des graphiques est disponible dans sur GitLab : https://gitlab.com/vberten/rarevalueanalysis/blob/master/RareValueAnalysis.ipynb

______________________

Remerciements à Gani Hamiti et Isabelle Boydens, pour les très fructueuses discussions qui ont mené à la rédaction de cet article.

Ce post est une contribution individuelle de Vandy Berten, Data Science Expert chez Smals Research. Cet article est écrit en son nom propre et n’impacte en rien le point de vue de Smals.