Met GDPR, van toepassing sinds mei 2018, voorschrijft de EU de regels voor de verwerking van persoonsgegevens door bedrijven en overheden van EU burgers. Om persoonlijke gegevens in een dataset te beschermen gaat men al te vaak de persoonlijke gegevens verwijderen of gebruikmaken van anonimiseringstechnieken. Het probleem is dat dergelijke technieken gevoelig zijn aan zogenaamde “data linkage” aanvallen waarbij de gegevens via ogenschijnlijk onschuldige attributen toch met persoonsgegevens van andere datasets verbonden kunnen worden. Een berucht voorbeeld is de anonieme dataset die Netflix voor een wedstrijd publiceerde en onderzoekers in staat waren deze, aan de hand van een tweede dataset, te de-anonimiseren. En zelfs als een bepaald datapunt zoals een rij in een tabel of een spreadsheet met meerdere personen overeenkomt, dan nog kan een analist (vaak een tegenstander genoemd) informatie afleiden. Dit scenario wordt in Tabel 1 geïllustreerd.

Tabel 1 Zelfs in een scenario waar een tegenstander op zoek is naar een specifieke persoon in een pseudo-geanonimiseerde[1] dataset waar er meerdere overeenkomsten mogelijk zijn, kan de tegenstander nuttige informatie afleiden. In dit scenario werd de persoon met de naam “Chris X.” via een reeks attributen (geboortejaar, postcode, etc.) met drie records in de geanonimiseerde dataset gelinkt. Als de tegenstander weet dat die persoon in de geanonimiseerde dataset voorkomt, dan weet hij dat Chris minstens een maandloon tussen de 1500,00 en 2500,00 EUR heeft, met een kans van 66% 1750,00 EUR of meer verdient, enz.
Ook kunnen updates doorheen de tijd informatie lekken. Dit illustreren we in Figuur 1 met een zeer eenvoudig voorbeeld, waar we de aantallen per categorie (e.g., personeelscategorie) bijhouden. Als een tegenstander weet dat een bedrijf drie nieuwe werknemers heeft aangeworven, dan kan de tegenstander afleiden over welke categorieën het gaat. Ook hier kan een tegenstander heel wat afleiden met achtergrondkennis of informatie omtrent personeelscategorieën die te vinden zouden zijn.
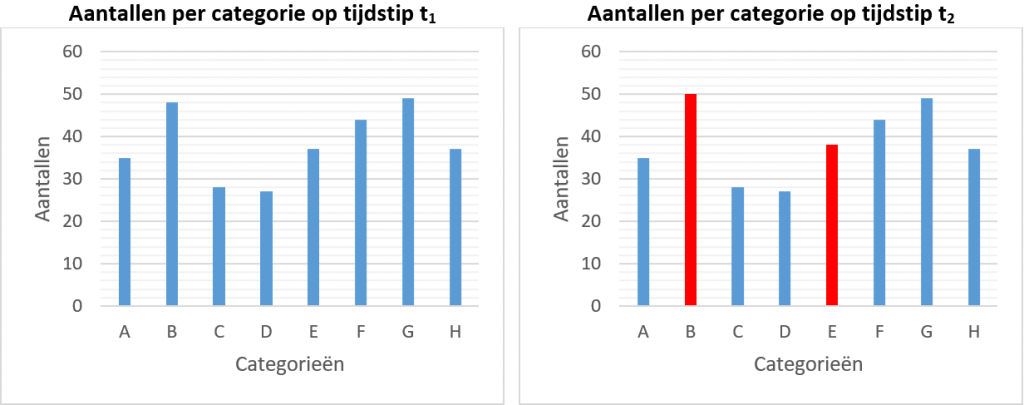
Figuur 1 Updates aan datasets doorheen de tijd zijn ook in staat gegevens te lekken.
Verder werd er aangetoond dat men via een reeks bevragingen (of queries) makkelijk informatie omtrent individuele datapunten en zelfs de hele dataset kan te weten komen. Men kreeg het inzicht dat privacy enkel gevrijwaard kan worden als er op een adequate wijze ruis in de data of de antwoorden op bevragingen wordt geïntroduceerd.
Een bepaald techniek om dit te realiseren heet Differential Privacy (DP). Het concept en onderliggende formalisme van DP werden voor het eerst gepubliceerd in 2006 (Dwork et al. 2006) en had een enorme impact. Privacy werd geformuleerd in termen van het algoritme dat ruis introduceert in plaats van in eigenschappen van een dataset.
Over de jaren heen werd het concept van nader bestudeerd en won velerlei prijzen. Recentelijk wordt DP alsmaar meer in de publieke en privésector toegepast, waardoor deze zelfs op de radar van Gartner kwam. De uitdagingen van DP zijn de beschikbare tooling (bibliotheken, raamwerken, etc.) en de kennis die nodig is om DP op een adequate manier toe te passen. Zoals we echter kunnen zien, duiken er alsmaar initiatieven op om DP toegankelijker te maken.
In een eerste instantie zullen we het principe visueel voorstellen. Om een idee te vormen waar en hoe DP wordt toegepast, zullen we een aantal voorbeelden uit de praktijk aanhalen. Nadien nemen we de wiskundige grondslag met net voldoende diepgang door om het principe beter te vatten. Er zijn ook een aantal varianten op DP, en zelfs varianten in diens toepassing. Varianten zullen in dit artikel niet behandeld worden.
Wat is differential privacy?
In Figuur 2 lichten we het principe eenvoudig toe. Waarom zou een persoon zijn informatie willen delen, of zelfs deze op een eerlijke manier willen delen? Een persoon wil namelijk niet dat het delen van diens informatie voor zichzelf onmiddellijke, mogelijk nefaste gevolgen heeft. Een klassiek voorbeeld is het mogelijk mislopen van bepaalde kansen zoals een hypothecaire lening.
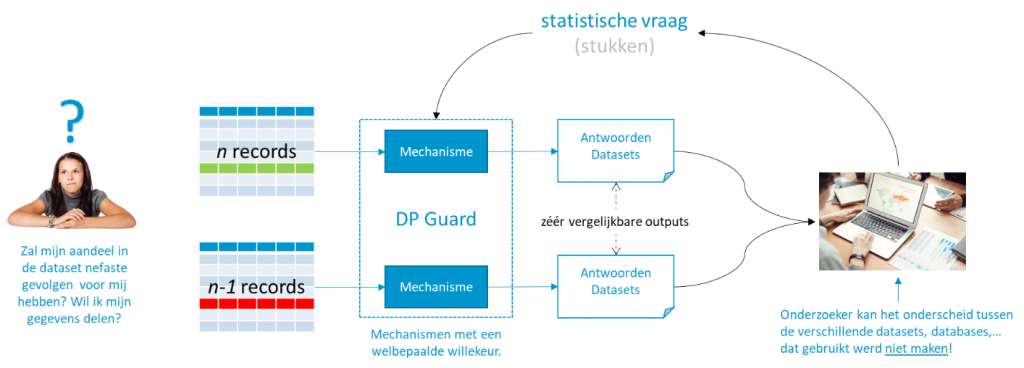
Figuur 2 Visuele representatie achter het principe van differential privacy.
Laten we aannemen dat we twee datasets hebben; één waar de gegevens van de persoon zijn opgeslagen, en één waar diens gegevens niet in voorkomen—ze verschillen dus in één record van elkaar. In DP wordt een methode voorgesteld waar een bevraging door een onderzoeker (of tegenstander) vergelijkbare antwoorden moet teruggeven, ongeacht welke dataset wordt gebruikt. Een onderzoeker wenst een vraag te laten beantwoorden en stuurt deze naar een systeem (al dan niet deels menselijk), die we een “DP Guard” noemen. Die guard consulteert de originele data om een antwoord te formuleren en maakt gebruik van een mechanisme om een welbepaalde willekeur in dat antwoord te introduceren. Die willekeur, onder andere bepaald door een privacy-parameter die de privacy loss bepaalt, moet aan DP voorwaarden voldoen. Het zijn namelijk die voorwaarden die er voor zorgen dat de antwoorden vergelijkbaar en de privacy gevrijwaard blijven. Belangrijk is dat de antwoorden dusdanig vergelijkbaar zijn dat een onderzoeker niet kan achterhalen welke dataset werd gebruikt.
Het principe achter DP is dat iemands deelname aan een dataset niet te achterhalen valt, en dat het eigenlijk ook niet uitmaakt. De antwoorden blijven grosso modo dezelfde, en dus ook de conclusies en inzichten die daaruit gehaald kunnen worden. Indien een persoon toch een lening niet zou krijgen, dan lag dit aan de hele dataset en niet aan die ene record.
De concepten van privacy en privacy loss (en andere termen die we zullen tegenkomen) zijn allemaal wiskundig onderbouwd en bewezen—we weten welke soorten willekeur voor welke soorten vragen aan de DP vereisten voldoen. De parameters maximaliseren niet alleen de bruikbaarheid en correctheid van de antwoorden, maar worden ook gebruikt om de privacy loss te berekenen. We gaan later zien hoe we daar een soort van “boekhouding” mee kunnen doen.
Dankzij de formele beschrijvingen van privacy, garandeert DP een aantal zaken. Ten eerste krijgt een onderzoeker de originele data nooit te zien. Ten tweede, is het, zonder kennis van de originele database, niet mogelijk om met post-processing de privacy loss op te krikken.
Toepassingen
We weten nu dat een mechanisme op een welbepaalde manier ruis in data en/of antwoorden kan introduceren. Details omtrent die ruis, en hoe deze kan ingesteld worden, zullen we pas in de volgende sectie behandelen.
In dit stukje van het artikel zullen we een aantal toepassingen van DP aanhalen. Een uitdaging van DP is dat het vaak voor specifieke doeleinden wordt toegepast (bijvoorbeeld om privacy in leeralgoritmes te vrijwaren). Hierdoor kan het moeilijk zijn om DP of diens toepassingen daarvan te veralgemenen of naar andere toepassingsgebieden te transponeren. Met de volgende drie toepassingen pogen we een brede waaier aan mogelijkheden toe te lichten.
- Microsoft Research ontwikkelde PrivTree. Hun doel was om de geolocaties van personen in databases te beschermen. Met andere woorden, hun doel was er voor te zorgen dat het gebruik van die geolocaties geen personen kan identificeren. Er zijn twee fasen in hun proces. In een eerste instantie delen ze de kaarten zodanig op zodat enige willekeur (ruis) die later toegevoegd zou worden de statistische eigenschappen van de databank zo goed als mogelijk bewaart. Men wilt bijvoorbeeld niet dat een verzameling punten dicht bij elkaar plots ver van elkaar worden verspreid (denk aan stadscentra versus woonwijken). In een tweede instantie wordt de ruis binnen elke partitie toegevoegd.
- Uber werkte samen met academici aan een oplossing voor DP. Ze wensten DP in hun data analyses te introduceren. Hun analisten maken voornamelijk gebruik van SQL om gegevens op te vragen. De oplossing die werd ontwikkeld had als oog om de bestaande infrastructuur te bewaren. Ze wensten geen beroep te doen op een softwarebibliotheek die DP in de resultaten injecteerden. In plaats daarvan, ontwikkelden ze een platform waar hun bestaande SQL queries automatisch werden herschreven (Johnson et al. 2020). Ze “injecteerden” als het ware DP in de queries. Op die manier hoefden analisten zich niet te veel zorgen maken over de technische aspecten van DP. Opmerkelijk was dat ze in staat waren om meer dan 90% van de duizenden queries die analisten hadden geformuleerd, te herschrijven.
- Apple gebruikt DP als onderdeel van hun service om populaire emoji’s te voorspellen. DP voorspelt de emoji’s natuurlijk niet, maar dit proces werd in de pijplijn geïntroduceerd om de privacy van gebruikers te vrijwaren. Interessant in dit voorbeeld is dat DP lokaal op iemands toestel werd toegepast. In tegenstelling tot de twee voorgaande voorbeelden waar data gecentraliseerd is en DP tijdens bevragingen werden toegepast, maken ze hier gebruik van DP in iemands data alvorens deze op te slaan. In zulk een setting gaat men er van uit dat men de gebruikers van het gecentraliseerde systeem niet kan vertrouwen; alle bevragingen en analyses maken sowieso gebruik van data met ruis.
Men kan nog aantal andere voorbeelden van DP aanhalen, maar deze drie voorbeelden geven al een vrij duidelijk plaatje waarvoor en hoe DP kan gebruikt worden; data analyses en AI (e.g., machine learning), met bibliotheken of een laag bovenop bestaande infrastructuur, op een lokale of gecentraliseerde wijze, enz. Men kan zich nu de vraag stellen hoe dit eigenlijk werkt.
Wiskundige grondslag
Hier lichten we het principe wat meer formeel toe. Een functie F voldoet aan DP voorwaarden en noemen we dus een mechanisme als voor alle mogelijke naburige datasets x en y (dat zijn datasets die zich in één rij verschillen), en voor alle mogelijke verzamelingen oplossingen van de functie F, die we OPL(F) zullen noemen, de volgende voorwaarde geldt:
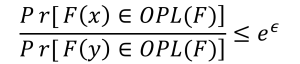
Waar e de wiskundige constante 2.7182 (afgerond) is. In deze voorwaarde is ε de privacy-parameter[2] en laat ons toe om het aandeel privacy te manipuleren.
- Hoe kleiner ε, hoe gelijkaardiger de outputs moeten zijn, dus hoe meer privacy;
- Hoe groter ε, hoe meer verschillend de outputs mogen zijn, met als resultaat minder privacy.
Deze formule zier er ingewikkelder uit dan het eigenlijk is. Deze formule legt een beperking op; namelijk dat de kansen (Pr in de figuur) dat alle koppels een bepaalde oplossing hebben op elkaar moeten lijken. En die gelijkwaardigheid wordt bepaald door ε. Verder is de voorwaarde symmetrisch omdat dit voor alle mogelijke paren van naburige datasets moet gelden. Dit principe wordt voor twee datasets in Figuur 3 op een zeer vereenvoudigde manier geïllustreerd.
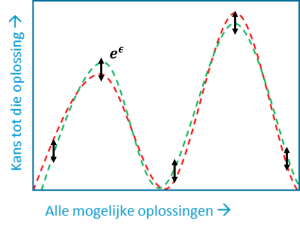
Figuur 3 De kans dat twee naburige datasets dezelfde oplossingen hebben moeten op elkaar lijken. Let op: de verhouding van alle kansen moet kleiner zijn dan eϵ. Met dit figuur wil ik enkel aantonen dat men het toegestane verschil “over de hele lijn” met ϵ kan configureren.
Wat is functie F dan? F is de functie met een welbepaalde willekeur (randomness) en het is die willekeur die aan DP voorwaarden moet voldoen. De verschillende soorten willekeur die al dan niet aan de voorwaarden voldoen werden bestudeerd. Een Gaussiaanse kansverdeling voldoet niet aan de voorwaarden, bijvoorbeeld, en een Laplace kansverdeling (voor telfuncties) wel. Waarom de ene kansverdeling wel voldoet aan de voorwaarden en de andere niet is voor dit artikel niet belangrijk. Belangrijk is om te weten dat de wetenschappelijke gemeenschap de DP eigenschappen voor verschillende soorten functies en kansverdelingen hebben bewezen.
Laten we het voorbeeld van een eenvoudige telfunctie nemen. Dit kan men vergelijken met een SELECT COUNT(*) query in SQL. De telfunctie F, met DP, ziet er dan als volgt uit:
![]()
In de formule is f de telfunctie die de “echte” waarde teruggeeft, dus de telfunctie zonder DP. In ons voorbeeld is f de eigenlijke SQL query die door een database management systeem wordt beantwoord. De gevoeligheid van een functie wordt voorgesteld door s. De gevoeligheid geeft ons een indicatie hoe gevoelig functies zijn wanneer datasets zich in één record verschillen. De gevoeligheid van een telfunctie is telkens één, want het aanpassen van één record levert ten hoogste een verschil van één op—je telt er ten hoogste één meer of ten hoogste één minder op. Tot slot geeft Lap een steekproef terug gebruikmakende van een Laplaceverdeling met verschuiving 0 en schaal s/ε.
In Figuur 4 ziet men duidelijk het effect van e. Hoe groter ε, hoe groter de kans dat de waarde van F(x) meer naar de waarde van f(x) zal neigen. Bij kleinere waarden voor ε zal de kans dat resultaten verder van elkaar liggen groter worden, wat de privacy verhoogt.
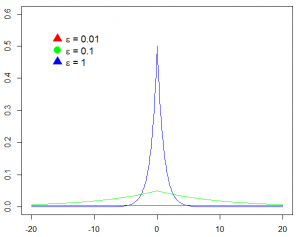
Figuur 4 Kansdichtheden van Laplace kansverdelingen met verschuiving 0 en schalen s/0.01, 1/0.1, en s/1, waar s=1. Hoe scherper de piek, hoe groter de kans dat waarden dichter bij de reële waarde zullen liggen. Waarden (ver) boven de 1 zijn doorgaans niet interessant en lekken veel informatie.
Hier volgt een concreet voorbeeld. Laten we aannemen dat de functie fb het aantal personen met een Belgische nationaliteit teruggeeft en de reële waarde van fb(x) gelijk is aan 5. We berekenen Fb(x) met ε = 0.1, dan als volgt: 5 + Lap(1/0.1). In dit voorbeeld gebruik ik de rlaplace functie uit R’s rmutil bibliotheek om een steekproef te genereren.
> library("rmutil")
> rlaplace(1, 0, 1 / 0.1)
[1] -0.5499616
Het eerste argument is het aantal waarden dat ik wil genereren; we hebben er maar één nodig. Het tweede argument is de verschuiving; hier altijd nul. En het laatste argument is de schaal. Als we dit aan 5 optellen, dan hebben we als resultaat Fb(x) = 4.4500384. We hebben nu ruis in de waarde geïntroduceerd. Was de reële waarde 4 en werd een waarde toegevoegd? Of was de reële waarde 5 en werd een waarde afgetrokken? Een tegenstander kan dit niet achterhalen. Een decimale waarde voor een telfunctie houdt natuurlijk geen steek. Later zien we dat enige verfijning, zoals het afronden van waarden, geen effect heeft—de ε-DP voorwaarde blijft behouden.
We hebben een mechanisme voor een telfunctie toegelicht. Er bestaan ook mechanismen voor, onder andere, histogrammen, het kruisen van informatie, en statistische benaderingen (steekproeven, aggregaties, gemiddelden, etc.). Deze zullen we hier niet toelichten.
DP vormt het basisprincipe, en er bestaan reeds een aantal varianten en uitbreidingen op dit principe. DP is “streng” en varianten zullen doorgaans aspecten van DP verzwakken, zoals Approximate DP, in ruil voor meer flexibiliteit en efficiëntie.
Privacy loss en privacy budgetten beheren—de “boekhouding”
Wat als een onderzoeker meerdere vragen stelt? Het is waar dat de garantie dat privacy gevrijwaard wordt daalt naarmate meer vragen worden gesteld. DP laat echter toe hier een stokje voor te steken. De formeel bewezen eigenschappen van compositie (i.e., het combineren van vragen) helpen ons om de totale kost van (een reeks van) bevragingen te berekenen.
De sequentiële compositie toont aan dat als F1 voldoet aan ε1-DP, en F2 voldoet aan ε2-DP, dan voldoet het mechanisme F3(x)=(F1(x), F2(x)) aan ε1+ε2-DP. Zo bestaan er andere composities (parallel, geavanceerd, etc.) die hier buiten beschouwing worden gelaten. Belangrijk is dat we met composities van de privacy parameters aan privacy “boekhouding” kunnen doen.
Eke vraag heeft dus een (privacy) kost, en men kan de totale kost gebruiken om op een bepaald moment geen antwoord meer te bieden aan een reeks vragen, of zelfs onderzoekers een totaal budget aan te bieden waarmee ze dan (zorgvuldig) aan de slag gaan. Hoe dit effectief in zijn werk gaat en hoe de budgetten naderhand bijgevuld worden hangen af van de use case.
Post-processing
We hebben reeds aangehaald dat het, zonder kennis van de originele database, niet mogelijk is om met post-processing de privacy loss op te krikken. Met andere woorden, elke aanpassing of wijziging aan een dataset die aan DP met een waarde voor ε voldoen, garandeert dus ook DP met dezelfde ε. Dit is een belangrijke en bewezen eigenschap van DP dat DP zo aantrekkelijk maakt.
Onder post-processing verstaan we niet alleen de manipulaties door een onderzoeker (of tegenstander), maar ook de post-processing net voor het aanleveren van de data. De ruis, geïntroduceerd door een mechanisme, kan waarden opleveren die niet stroken met de realiteit. Voorbeelden zijn decimale en negatieve waarden bij telfuncties. Het is dus perfect OK om een dataset nadien te verfijnen om dergelijke “datakwaliteitsproblemen” aan te pakken. Het verfijnen van een dataset (zoals het afronden en elimineren van negatieve waarden waar nodig) hoort ook tot post-processing.
Aan de slag met DP
DP heeft een stevige wiskundige onderbouwing, doch is het interessant om weten dat maar recentelijk de industrie en de gemeenschap dit in grotere mate aan het oppikken is. Tot voor kort was één van de uitdagingen het bestaan van tooling (raamwerken en bibliotheken). Men moest dus beroep doen op personen met de juiste expertise (e.g., een statisticus) die data volgens DP voorwaarden leverden. Met de recente ontwikkelingen kwamen gelukkig ook een aantal open source alternatieve van grote en belangrijke spelers: onder andere Google, Facebook, Uber, en Harvard. Microsoft documenteerde hoe je Harvard’s oplossing kan gebruiken in MS Azure.
Voor dit artikel maak ik gebruik van Chorus. Chorus startte als samenwerking tussen Uber en de University of California, Berkeley. Omdat academici nu eenmaal regelmatig van instelling veranderen, wordt de code (beschikbaar met een zeer toegankelijke MIT licentie) nu onder “hoedanigheid” van de University of Vermont gehost.
Gebruikmakende van een tabel met 1001 fictieve personen (er waren geen personen met als land België aanwezig, dus heb ik er maar eentje toegevoegd), wens ik te weten hoeveel personen in België wonen, en hoeveel in (Volksrepubliek) China.
SELECT COUNT(*) FROM person WHERE country = 'China'SELECT COUNT(*) FROM person WHERE country = 'Belgium'
De waarden van deze queries, alsook die met DP gebruikmakende van Chorus staan in Tabel 2. Zonder DP hebben we als reële waarden 181 en 1. Met een ε van 0.1 hebben we meer privacy, want de kans is groter dat de waarden verder van de reële waarden verwijderd zijn. Met een ε van 1 vergroten we de kans dat de waarden meer op de reële waarden lijken.
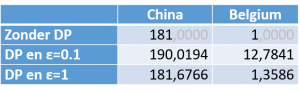
Tabel 2 Resultaten van tel-queries met Chorus. Merk dat grotere waarden voor ε de kansen dat de waarden meer naar de eigenlijke waarden “neigen” verhogen. Vanwege de willekeur, is de kans bijzonder klein dat men tweemaal hetzelfde antwoord terugkrijgt.
Men kan nu denken dat men met een ε = 1 met zekerheid de juiste waarden kan achterhalen door deze gewoon af te ronden, maar dat is niet correct. Zelfs als de onderzoeker (of tegenstander) weet dat ε = 1 en de kans groter is dat de waarde op de reële waarde lijkt, is de exacte waarde moeilijk te achterhalen. De ruis kan zowel positief als negatief zijn. Verder kan deze afwijking nog vrij belangrijk zijn. Ik illustreer dit met een voorbeeld in Figuur 5.

Figuur 5 De uiteenlopende waarden voor ruis (niet exhaustief (!)) voor de Laplacekansverdeling met schaalverdeling 1/1=1.
De kans op eenzelfde antwoord (bij het bevragen van dezelfde query) is dus ook klein. Dit illustreer ik nogmaals in Figuur 6 (onderaan), waar we voor ε = 1 nu de waarden 181.182 en 3.369 voor onze tel-queries hebben.
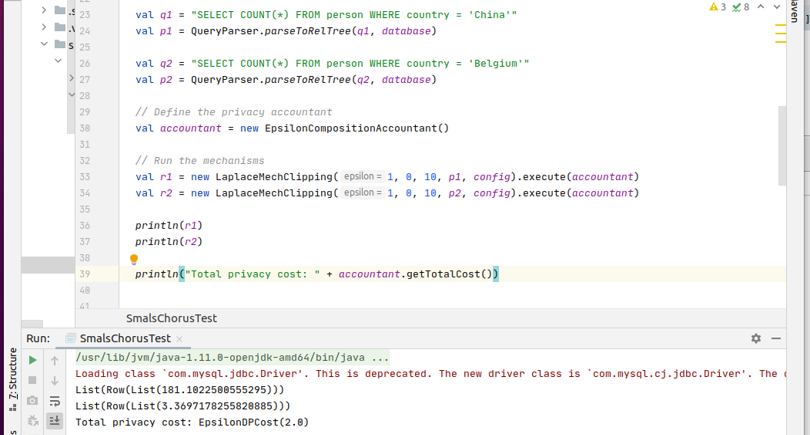
Figuur 6 Gebruik van Chorus voor het bevragen van een MySQL databank. Merk op dat de waarden onderaan, vanwege de willekeur, verschillen met de waarden in Tabel 2.
Het opzetten en gebruiken van Chorus was best eenvoudig. Het systeem ondersteunt standaard simpele queries—queries die maar één waarde teruggeven. Dit omdat queries die meerdere waarden teruggeven (bijvoorbeeld een histogram of een GROUP BY) meer aandacht vergen. Voeren we een GROUP BY op namen uit, dan lekken we de namen in de database! Dit vergt dus manueel nazicht.
DP toepassen op onderstaande histogram query vormt geen probleem, want we tonen enkel landsnamen en hun aantallen. Gaat dan, voor elk land, de privacy cost omhoog? Neen. Dergelijke histogrammen voldoen aan parallelle compositie, waardoor de kost dezelfde blijft. De reden waarom dit geldt is, zéér kort samengevat, dat elk individu in de dataset maar één keer geteld wordt.
-
SELECT country, COUNT(*) FROM person GROUP BY country
Chorus biedt een oplossing aan om SQL queries, in de achtergrond, te herschrijven naar queries met ruis. Ook biedt het een zogenaamde accountant aan die de kost van een reeks queries berekent. Hoe je die kost gebruikt, wordt niet door Chorus voorgeschreven. Ook dit hangt van af van de use case.
Uitdagingen en opportuniteiten
Veruit de grootste uitdaging van DP is de kennis en expertise die men nodig heeft om DP op een correcte manier toe te passen. Niet alleen kennis van DP (de wiskundige grondslag), maar ook domeinkennis is nodig. Domeinkennis is nodig om, voor bepaalde mechanismen, doordachte beslissingen over de data te nemen zoals het bepalen van boven- en ondergrenzen voor bepaalde attributen. De aanwezigheid van uitschieters geeft informatie over de dataset, maar kan ook de ruis vertekenen. Computerwetenschappers (of statistici) moeten hieromtrent met business analisten samenwerken, dus.
DP werd ook toegespitst voor zeer specifieke doeleinden (gaande van specifieke toepassingen zoals het voorspellen van emoji’s tot specifieke taken zoals DP in leeralgoritmen). Dit maakt het voor buitenstaanders soms moeilijk om DP naar andere use cases te transponeren.
Daartegen staat dat, dankzij de solide wiskundige onderbouwing, het ook duidelijk is welke bevragingen “makkelijk” zijn, en welke op een doordachte manier moeten gebeuren. Eenvoudige queries die 1 waarde teruggeven, zoals onze tel-queries bijvoorbeeld, kunnen zonder problemen automatisch uitgevoerd worden. Het genereren van histogrammen vergt menselijke input (de query, code en parameters moeten uitgeschreven worden), én nazicht. In eenvoudige gevallen kan men dit “omzeilen” door onderstaande histogram
-
SELECT country, COUNT(*) FROM person GROUP BY country
te herschrijven naar:
SELECT COUNT(*) FROM person WHERE country = 'Belgium'SELECT COUNT(*) FROM person WHERE country = 'France'SELECT COUNT(*) FROM person WHERE country = 'Germany'…
Doch verhogen we in het tweede scenario onnodig de privacy cost, want voor histogrammen blijft de kost, vanwege de parallelle compositie, gelijk. De boodschap hier is dat de drempel voor DP laag kan zijn.
De tweede uitdaging is de beschikbare tooling. Tot voor kort werd DP door experten toegepast. Er bestaan commerciële toepassingen voor machine learning en data analytics waarin DP werd geïntegreerd, maar niet iedereen is op zoek naar dergelijke oplossingen of klaar om naar een nieuwe toepassing over te schakelen. Organisaties wensen vaak ook hun bestaande systemen te behouden. Men kan DP toepassen in Python, R,… door de datamanipulatie en formules zelf neer te pennen, maar gelukkig verschijnt er alsmaar meer robuuste vrije software (aangeleverd door de voorgenoemde grote spelers). Men kan twee soorten initiatieven onderscheiden: “wrappers” die men bovenop bestaande databases kan plaatsen, zoals Chorus; en bibliotheken met abstracties en primitieven om DP in big data en data analytics omgevingen toe te passen, zoals Google’s Privacy on Beam.
Conclusies
Differential Privacy (DP) is een techniek om de privacy van personen te vrijwaren door een welbepaalde ruis in datasets en antwoorden van bevragingen te introduceren. De antwoorden op die bevragingen alsook de statistische eigenschappen van de dataset blijven grosso modo onveranderd en men krijgt nooit de originele data te zien. De aanwezigheid van de gegevens van een persoon heeft dus geen (grote) impact op de conclusies die men kan trekken.
DP introduceert ook concepten zoals privacy cost en privacy budget. Men kan met een bepaald budget een of meerdere bevragingen uitvoeren. Elke bevraging heeft een kost en men mag het budget niet overschrijden. Wenst men dat de resultaten dichter bij de reële waarden komen, dan moet men meer uit het budget gebruiken. Dit gaat dan ten koste van het aantal (grote) queries die men in een sessie kan stellen. Hoelang sessies duren, hoe snel men een budget terug kan opbouwen, enz. hangt af van de use case. Dit brengt ons naar het volgende punt.
Vanwege de complexe materie is enige kennis in DP én domeinkennis voor complexe vragen vereist. Voor eenvoudige vragen kan men DP zo goed als volledig automatisch toepassen. Computerwetenschappers, statistici, en bedrijfsanalisten moeten in het proces betrokken worden.
Hoewel het concept in 2006 werd geïntroduceerd, is het maar sinds kort dat tal van initiatieven opduiken. Dankzij de wetenschappelijke gemeenschap, de open source community, en belangrijke IT spelers die hun tooling vrij voorhanden maken, wordt de drempel om DP toe te passen lager.
Referenties
Dwork, Cynthia, Frank McSherry, Kobbi Nissim, and Adam Smith. 2006. “Calibrating Noise to Sensitivity in Private Data Analysis.” In Theory of Cryptography, eds. Shai Halevi and Tal Rabin. Berlin, Heidelberg: Springer Berlin Heidelberg, 265–84.
Johnson, Noah M, Joseph P Near, Joseph M Hellerstein, and Dawn Song. 2020. “Chorus: A Programming Framework for Building Scalable Differential Privacy Mechanisms.” In IEEE European Symposium on Security and Privacy, EuroS&P 2020, Genoa, Italy, September 7-11, 2020, IEEE, 535–51. https://doi.org/10.1109/EuroSP48549.2020.00041.
Voetnoten
[1] In de context van GDPR hebben “geanonimiseerd” en “pseudo-geanonimiseerd” (ofte “pseudonimisatie”) verschillende betekenissen. Het eerste gaat over data waar het herleiden van gegevens tot een natuurlijk persoon onmogelijk is. Het tweede betreft data waar men met behulp van extra gegevens (op een indirecte manier) informatie naar een natuurlijk persoon kan herleiden.
[2] Soms ook privacy-budget genoemd, dit hangt af van het gebruik (zie later).
Foto’s
Foto’s verwerkt in de illustraties zijn CC0 (via https://www.pexels.com/).
_________________________
Dit is een ingezonden bijdrage van Christophe Debruyne, IT consultant bij Smals Research. Dit artikel werd geschreven in eigen naam en neemt geen standpunt in namens Smals.

Leave a Reply