Dans l’article précédent, nous expliquions plusieurs scénarios dans lesquels des données de type “réseau” (à savoir un ensemble d’entités ou nœuds, comme des personnes ou des sociétés, reliées par un ensemble de liens ou relations, comme une relation de travail ou un lien d’amitié) sont collectées, et dans lesquels on cherche à identifier soit des structures particulières (comme dans le cas de spider constructions), soit des entités ayant des caractéristiques définies.
L’analyse de réseau (souvent appelée en anglais social network analytics) reprend l’ensemble des techniques algorithmiques permettant d’extraire certaines informations utiles à partir des données d’un réseau. Nous allons ici présenter quelques éléments de base de ce type d’analyse.
Simplifier
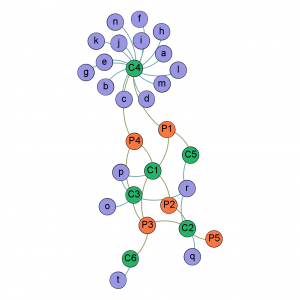
Réseau composé de personnes suspectes (P1-P5, orange), leurs employeurs (C1-C6, verts), les autres employés de ces employeyrs (a-t, bleu).
Lorsqu’un organisme de contrôle (inspecteurs fiscaux ou sociaux, services de police ou de renseignements) collecte des données “réseau”, il est rapidement confronté à un volume très important de données. Supposons que l’organisme en question ait 5 personnes dans le collimateur (P1-P5, en orange dans le réseau ci-contre), soupçonnées d’activités criminelles ou frauduleuses dans le cadre de leur travail, et voudrait d’une part déterminer les liens qui existent entre ces 5 personnes, et d’autre part identifier d’autres personnes qui pourraient être très proches de suspects, et mériteraient donc une attention particulière.
Une façon simple de faire serait de s’intéresser aux employeurs (présents et passés, en vert) de ces 5 personnes, puis à tous les autres employés de ces employeurs (en bleu, de “a” à “r”). Cela permettrait d’identifier des collègues en commun, et de voir à quel point les autres collègues sont liés.
Supprimer les super-connecteurs
Le problème d’une telle recherche est que si l’un des suspects a travaillé pour une très grosse entreprise (un ministère, une société de transport public, une grande chaîne de magasin…), ce nœud va faire exploser la taille du réseau, le rendant totalement inexploitable.
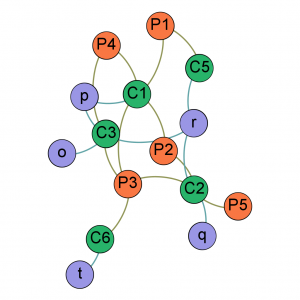
Réseau original après la suppression du super-connecteur “C4”, en ne gardant que la composante connexe principale.
Un exemple similaire apparaît si l’on veut retrouver des couples d’entreprises prétendument distinctes mais n’étant séparées que fictivement, en se basant entre autres sur leur adresse : certaines tours de bureaux dans des grandes villes sont parfois le siège social de plus de 1000 entreprises.
Une technique classique consiste alors à ignorer de tels nœuds (entreprise, adresse), que l’on peut qualifier de super-connecteurs, ou à tout le moins de les masquer provisoirement. On y perd potentiellement des informations importantes, mais l’on rend le reste du réseau exploitable. Moins d’information donc, mais plus de valeur.
Typiquement, la suppression de ces super-connecteurs va avoir pour conséquence de diviser le réseau en plus petits groupes, appelés “composantes connexes”, qui pourront être étudiées individuellement (cf image ci-dessus, où seule la plus grande composante connexe a été gardée).
Techniquement parlant, le degré d’un nœud désigne le nombre de ses relations. Par exemple, le degré d’un nœud “Travailleur” sera le nombre de ses employés, et le degré d’un nœud “Entreprise” correspondra au nombre de ses travailleurs. Les super-connecteurs sont donc des nœuds avec un haut degré.
Supprimer les feuilles isolées
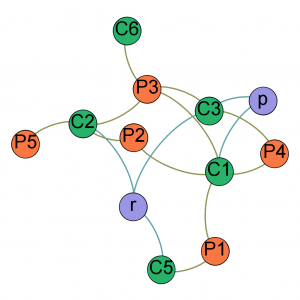
À l’autre extrémité, une “feuille”, c’est-à-dire un nœud de degré 1, connecté à un et un seul nœud, a souvent peu de valeur lorsque l’on veut établir des connexions entre des personnes ou d’autres entités. Il est souvent intéressant, en tout cas dans une phase de l’analyse, d’éliminer toutes les feuilles qui ne sont pas les nœuds à l’origine de l’analyse (les 5 individus évoqués ci-dessus, dans l’exemple cité). L’image ci-contre illustre ce filtre. Avec ce filtre, il ne reste que deux “nouveaux collègues”. On voit en particulier que “r” a été collègue avec chacun des nœuds orange, via les sociétés C2, C3 et C5, et mérite peut-être une attention particulière.
On peut même aller plus loin si on veut observer uniquement la “colonne vertébrale” d’un réseau, à savoir uniquement les nœuds principaux : on supprime alors tous les deux de degré inférieur à une valeur définie.
Une technique alternative, appelée “k-core”, consiste à supprimer tous les nœuds de degré 1 (plus généralement, de degré k). De ce fait, des nœuds, qui avant avait un degré deux, mais étaient connectés à un nœud que l’on vient de supprimer, se retrouvent avec un degré de 1 (par exemple C6 dans la figure ci-dessus). Le filtre “k-core” les supprime également, jusqu’à ce que plus aucun nœud du réseau n’ait un degré inférieur à deux (plus généralement k+1).
Distance
Après avoir collecté une série de nœuds et relations (provenant éventuellement de plusieurs sources), on peut se demander si deux individus, deux entreprises, deux organisations… ont des chances d’être en contact, même s’il n’existe pas de relation directe entre les deux. Différentes notions de “distance” permettent d’évaluer la proximité entre deux nœuds d’un réseau.
Plus court chemin
La mesure de la distance la plus classique consiste à compter le nombre minimum de relations qu’il faut parcourir pour joindre deux nœuds. Dans l’exemple ci-dessus, le travailleur P1 et son entreprise C1 sont à une distance de 1, deux collègues seront à une distance de 2, et P3 et C5 à une distance de 3. On parle de nœuds voisins pour désigner deux nœuds séparés d’une distance 1.
Différent algorithmes, dont les plus connus sont Dijkstra et A*, permettent de calculer efficacement cette distance.
Similarité de Jaccard
La similarité de Jaccard entre deux nœuds N1 et N2 d’un réseau désigne le ratio entre le nombre de nœuds étant des voisins communs de N1 et N2, et le nombre total de voisins de N1 et N2. Si l’on parle d’un réseau d’amitié comme Facebook, une similarité de Jaccard de 1 entre deux personnes signifierait que tous leurs amis sont communs, c’est-à-dire qu’aucun des deux n’a d’ami qui n’est pas également ami avec l’autre. Une similarité de 0 indique que deux personnes n’ont aucun ami en commun. Dans l’exemple de Facebook, une similarité élevée indique qu’il y a beaucoup de chances que les deux individus se connaissent, même s’ils ne sont pas “amis Facebook”. En d’autres termes, si deux personnes ont 1000 amis chacun sur un réseau social, mais seulement 50 en commun, ils seront considérés comme moins proches que deux personnes ayant chacun 100 amis, dont 50 en commun.
Dans notre exemple tout en haut de la page, P1 et P4 ont une similarité de Jaccard de 0,5 (2 voisins communs – C1 et C4 – et 4 au total – C1, C3, C4, C5), alors que P2 et P3 ont une similarité de 0.25 (1 voisin commun, 4 au total). Alors qu’en terme de distance simple, P1 et P4 sont séparés, comme P2 et P3, d’une distance de 2, la similarité de Jaccard nous enseigne que le premier couple est plus similaire que le second.
Centralité
Dans un réseau, tous les nœuds n’ont pas le même poids, la même importance. Il existe plusieurs façons de mesurer ce que l’on appelle la “centralité” d’un nœud. La mesure la plus simple, la “centralité de degré“, consiste à dire qu’un nœud de degré plus important est plus central. La “centralité d’intermédiarité” (betweenness centrality) évalue elle à quel point un nœud sert d’intermédiaire entre les autres nœuds. Le “PageRank” de Google est également un algorithme de centralité : il consiste à considérer que la centralité se diffuse via les liens. Si une page web importante A possède un lien vers une autre page web B, B héritera d’une partie de l’importance de A.
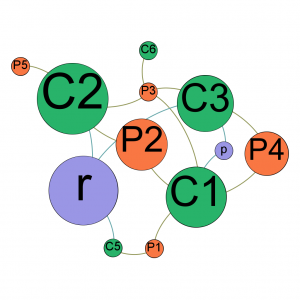
L’illustration ci-contre adapte la taille des nœuds en fonction de leur “betweenness centrality”. On y voit que le nœud “r” évoqué ci-dessus attire particulièrement l’attention par sa position centrale dans le réseau (en tant qu’intermédiaire).
Pour conclure
Si cet article présente l’utilisation de l’analyse de réseau dans le cas de la fraude, son utilisation est beaucoup plus large que ça. Elle permet également de modéliser des réseaux d’ordinateurs ou de télécommunication (serveurs/routeurs reliés entre eux par des câbles ou autre), des processus d’entreprises (tel service transmet tel document/demande/formulaire à tel autre service), d’usinage (une machine reçoit certaines pièces, produit une nouvelle pièce qui transite vers une autre machine), ou pour des analyses plus conceptuelles (liens entre des langues, des lois, des idées politiques…).
Il va de soi que les techniques utilisées en réalité sont beaucoup plus complexes que ce qui est présenté ci-dessus, ultra-simplifié à des fins pédagogiques. Mais la philosophie reste la même.
Illustrations réalisée avec Gephi (www.gephi.org)

Leave a Reply