Lorsque l’on s’intéresse à la situation socio-économique d’un pays, on est souvent amené à comparer des indicateurs pour savoir s’ils sont corrélés : existe-t-il une corrélation entre le niveau d’éducation et le revenu ? Entre les taux d’emploi et de criminalité ? Entre le niveau de pollution et la morbidité ? Il peut également être révélateur d’évaluer à quel point un indicateur d’un territoire (une commune, un quartier…) est corrélé à la valeur de ce même indicateur dans les territoires voisins. C’est ce qu’on appelle l’autocorrélation spatiale : sachant qu’une commune a un salaire moyen élevé, à quel point ses communes voisines ont-elles une chance d’avoir également un salaire élevé ? En d’autres mots, le salaire moyen a-t-il une composante géographique ? Dans cet article, accompagné d’un notebook Python, nous allons montrer plusieurs méthodes permettant d’évaluer cette dépendance spatiale.

Pour ce faire, nous allons récolter une série d’indicateurs à propos des 581 communes de Belgique, disponibles en open-source, sur https://statbel.fgov.be, https://data.belgium.be ou encore https://www.census2011.be.

Corrélation “classique”

Pour comprendre l’autocorrélation spatiale, il est nécessaire de d’abord bien saisir celui de corrélation statistique au sens “classique” du terme. Dans sa version de base (corrélation linéaire entre deux variables quantitatives), on peut évaluer visuellement la corrélation entre deux variables en les représentant sous forme de nuage de points (scatterplot). 

On y observe une corrélation assez claire : plus un des indicateurs est élevé, plus l’autre a des chances de l’être également. Ceci est formalisé par le coefficient de Pearson, qui vaut ici 0.79, indicateur entre -1 et 1, valant 1 si la connaissance d’une valeur permet de déterminer exactement la valeur de l’autre, avec une relation croissante (-1 si la relation est décroissante), 0 s’il n’existe aucune corrélation (linéaire) entre les deux variables. Notons qu’il ne faut pas commettre le sophisme Cum hoc ergo propter hoc : la corrélation entre deux variables n’indique pas nécessairement une relation de causalité entre les deux.

Avant tout : visualiser

En analyse de données, une des premières choses à faire avant de se lancer dans une analyse statistique complexe, est de visualiser les données. On se concentre maintenant sur une seule variable : dans la suite de cet article, nous analyserons le revenu moyen par commune (d’autres indicateurs sont disponibles dans le notebook évoqué dans l’introduction).

 

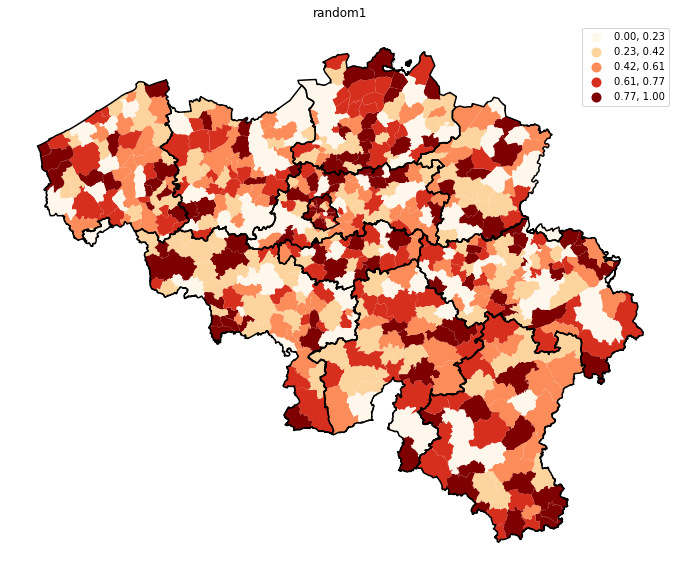
Dans les deux cartes ci-dessus, celle de gauche représente une valeur aléatoire assignée à chaque commune, alors que celle de droite montre le revenu moyen. Il saute clairement aux yeux que cette dernière variable a une composante géographique forte : le nord de Bruxelles est caractérisé par des faibles revenus (couleur claire), alors que le sud et le pourtour Bruxellois, comme les communes proches du Luxembourg, offrent des salaires élevés. Mais cette approche visuelle, bien que puissante, ne permet pas, par exemple, de savoir si la composante géographique du revenu est plus forte que celle de taux de diplômés. Ni d’identifier facilement s’il existe des zones où la dépendance spatiale est plus fortes que d’autres. Les approches suivantes nous permettront de le faire.

Décalage spatial (spatial lag)

Le “spatial lag” (ou décalage spatial) d’un secteur (dans notre cas, une commune) se calcule en effectuant la moyenne de la valeur considérée sur tous les secteurs voisins. 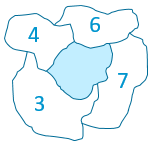Dans la figure ci-contre, le “spatial lag” du secteur bleu sera de 5 (la moyenne de 3, 4, 6 et 7, sans tenir compte de la valeur du secteur lui-même). Notons que ceci ne peut pas se calculer simplement sur base d’une liste contenant l’indicateur pour chaque secteur : il faut également connaitre la géographie, pour savoir quels sont les voisins de chaque secteur. Les détails de ce calcul sont donnés dans le notebook joint. Une fois le spatial lag calculé pour chaque commune, on peut réaliser un nuage de point de Moran, en positionnant chaque commune selon sa valeur sur l’axe horizontal, et le décalage spatial de cette même valeur sur l’axe vertical, comme illustré ci-dessous.

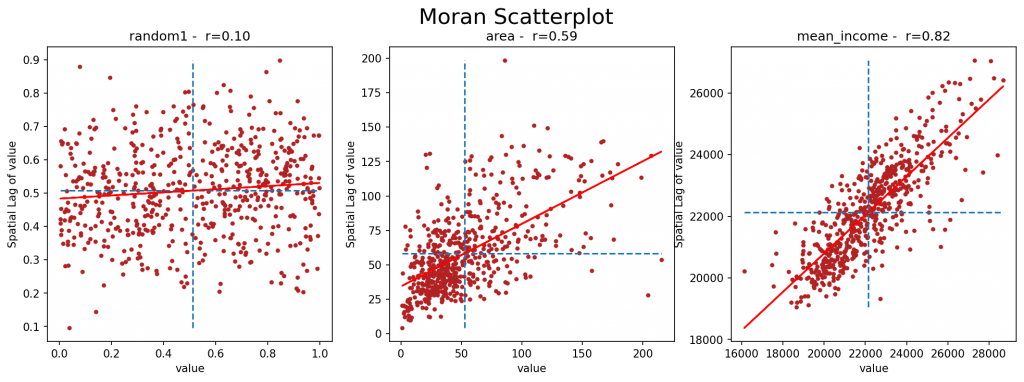
Le graphique de gauche illustre une valeur aléatoire. On peut y voir que, assez naturellement, aucune corrélation ne peut être établie entre la valeur d’une commune et la valeur moyenne de son voisinage. Celle de droite concerne le revenu moyen, et une corrélation forte y apparaît, confirmant une importante dépendance spatiale pour cette métrique. La valeur centrale se rapport à la superficie d’une commune. On y voit qu’une petite commune a plutôt tendance à être entourée de petites communes (coefficient de Pearson : 0.59), bien qu’il y ait quelques “anomalies”, mais avec une corrélation moins marquée que pour le revenu moyen (coefficient de Pearson : 0.82). 

Les lignes en pointillées représentent la moyenne de la valeur (verticale) et du décalage spatial (horizontale). Elle découpe donc le graphique en quatre quadrants : celui en haut à droite reprend les communes avec un haut revenu (plus élevé que la moyenne) entourées de communes avec un haut revenu, bien plus nombreuses que celles en bas à droite, communes avec un haut revenu entourées de communes avec un bas revenu.

Autocorrélation globale

La méthode de “Join Count” vise à résumer le degré d’autocorrélation par une métrique. Celle-ci s’établit de la façon suivante : on attribue premièrement à chaque secteur une valeur binaire, valant “Black” si la valeur est supérieure à la valeur médiane, et “White” si elle est inférieure. On va ensuite compter le nombre de “jonction Black-Black”, c’est-à-dire le nombre de situations où une commune “Black” touche une autre commune “Black”. Dans le cas du revenu moyen, ce comptage vaut 646. Cette valeur est-elle élevée ? Pour le savoir, on va exécuter un grand nombre de tirages aléatoires, dans lequel on attribuera aléatoirement les valeurs “Black” et “White” à l’ensemble des secteurs, pour ensuite en compter le nombre de jonctions “Black-Black” de chacun de ces tirages.  

Ces nombreux tirages (souvent de l’ordre de 1000), permettent d’obtenir une distribution, présentée ci-contre sous forme de cloche bleue.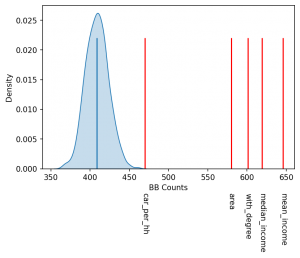 Les lignes horizontales rouges (dont la hauteur n’a pas d’importance) représentent les comptages pour les différentes métriques que nous avons considérées : salaire moyen (mean_income) ou médian (median_income), proportion de la population avec un diplôme (with_degree), superficie (area), ou nombre moyen de voitures par ménage (car_per_hh). Plus la métrique s’éloigne de la gaussienne, plus faible est la probabilité qu’elle ait été obtenue par un tirage aléatoire, et donc plus forte est sa composante spatiale.

Autocorrélation locale

La métrique globale présentée ci-dessus caractérise l’ensemble du territoire selon sa dépendance spatiale. Mais elle ne permet pas de mettre en évidence des parties du territoire qui seraient plus spatialement dépendantes que d’autres. On peut également (nous passons les détails techniques, qui sont donnés dans le notebook associé), avec une généralisation (également due au statisticien Moran)  des techniques présentées ci-dessus, associer à chaque secteur (entre autres) deux valeurs : 

• Le “quadrant”, déjà présenté ci-dessus, qui indique que le secteur a une valeur haute ou basse, entouré de valeurs hautes ou basses ;
• Une “p-value”, qui indique à quel point la valeur a des chances d’être issue d’un tirage aléatoire. Entre d’autres mots, à quel point ce secteur est corrélé à son voisinage.

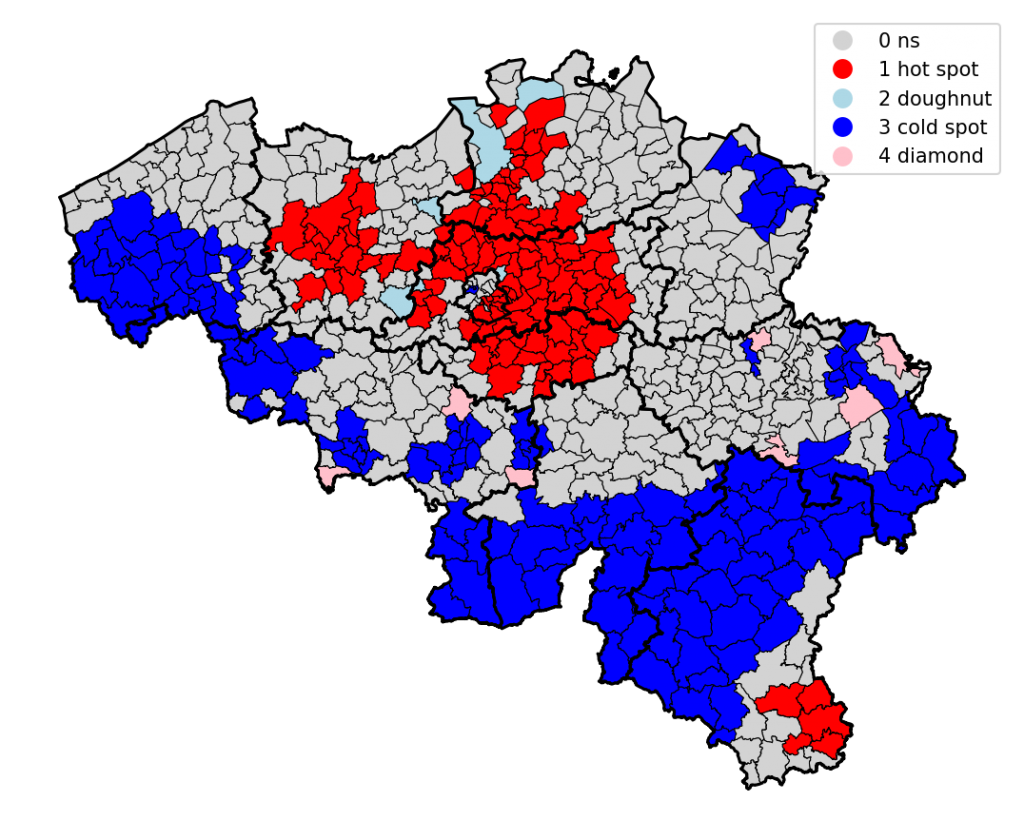
Ces deux valeurs permettent de construire la carte ci-dessous, où on retrouve : 

• En gris, les zones avec une “trop grande p-value”, c’est-à-dire où la composante spatiale n’est pas assez significative ;
• En rouge les “hot spots”, soit les communes à haut salaire, entourées de communes à haut salaire ;
• En bleu les “cold pots”, idem pour les communes à bas salaire ;
• En rose, les “diamonds”, les communes à haut salaire entourées de commune à bas salaire ;
• En bleu pâle, les “doughnuts”, les communes à bas salaire entourées de communes à haut salaire.

Conclusions

L’autocorrélation spatiale a de multiples applications. On peut par exemple évaluer la composante géographique du taux de mortalité dû à une maladie spécifique, en la comparant à la même analyse appliquée à la présence d’un polluant ou d’un certain type d’industrie ou d’infrastructure. Par ailleurs, il est aussi possible d’étendre l’analyse non plus à des polygones, mais à des points (commerces, chantiers, voire adresses d’individus) pour mettre en évidence des anomalies (“diamonds” ou “doughnuts”) selon une métrique pour laquelle on s’attend à voir une dépendance spatiale forte.

Il est également possible d’évaluer la corrélation entre deux variables, en tenant compte de leur composante géographique : ceci se fait classiquement en étudiant la corrélation (classique) entre une variable et le décalage spatial de l’autre variable (Bivariate Moran’s I).

Il est possible, comme dans le notebook joint, de faire cette analyse en Python, avec quelques librairies spécialisées (geopandas, libpysal, esda). Mais certains outils OpenSource, comme GeoDa, offrent une interface graphique permettant d’effectuer un grand nombre d’algorithmes d’analytique spatiale, dont l’autocorrélation spatiale.

Il faut cependant être attentif au fait que, tout comme la corrélation statistique en deux variables n’implique pas la causalité de l’une sur l’autre, la présence d’une forte autocorrélation spatiale ne permettra pas non plus de conclure automatiquement que la zone géographique impacte directement la variable étudiée A. Il se peut par exemple qu’une variable intermédiaire B soit, elle, impactée par la géographie, et qu’il existe une corrélation entre A et B. Établir une (auto)corrélation n’est jamais que le point de départ ; il est ensuite nécessaire d’observer les choses de façon plus globale pour établir les liens de cause à effet.

 

---

Ce post est une contribution individuelle de Vandy Berten, spécialisé en data science chez Smals Research. Cet article est écrit en son nom propre et n’impacte en rien le point de vue de Smals.