Dans un précédent article, nous avons introduit la cryptographie sur courbe elliptique (Elliptic Curve Cryptography (ECC) en anglais), l’aspect d’une courbe elliptique, et en quoi l’ECDLP est le fondement de la sécurité de l’ECC. Ici, nous allons voir comment l’ECC fonctionne en pratique. Encore une fois, je remercie par avance les experts dans le domaine qui comprendront qu’il n’est pas possible de rentrer dans les détails lorsqu’on souhaite présenter l’ECC aux non-initiés.
Comment fait-on des calculs sur une courbe elliptique?
Précédemment, nous avons vu la possibilité d’effectuer deux opérations mathématiques bien précises sur les courbes elliptiques :
- L’addition de points : quand on a deux points P et R sur une courbe elliptique EC, alors on peut calculer leur addition Q = P + R, et le résultat Q appartient aussi à EC.
- La multiplication de points : quand on a un point P sur une courbe elliptique EC, alors on peut additionner k fois ce même point (p.ex. si k = 2, alors on peut calculer P + P), ce qui résulte en la multiplication de points Q = k*P (p.ex. si k = 2, alors Q = 2*P = P + P), et le résultat Q appartient aussi à EC.
Finalement, la multiplication de points n’est qu’une simple série d’additions de points. Par exemple :
Q = 3*P = P + P + P = (P + P) + P.
Si on considère que T = P + P, alors on peut remplacer P + P par T dans l’équation précédente, ce qui revient à écrire que Q = T + P.
Graphiquement, l’addition de points (tant pour la simple addition que pour la multiplication de points) peut se dérouler des façons suivantes.
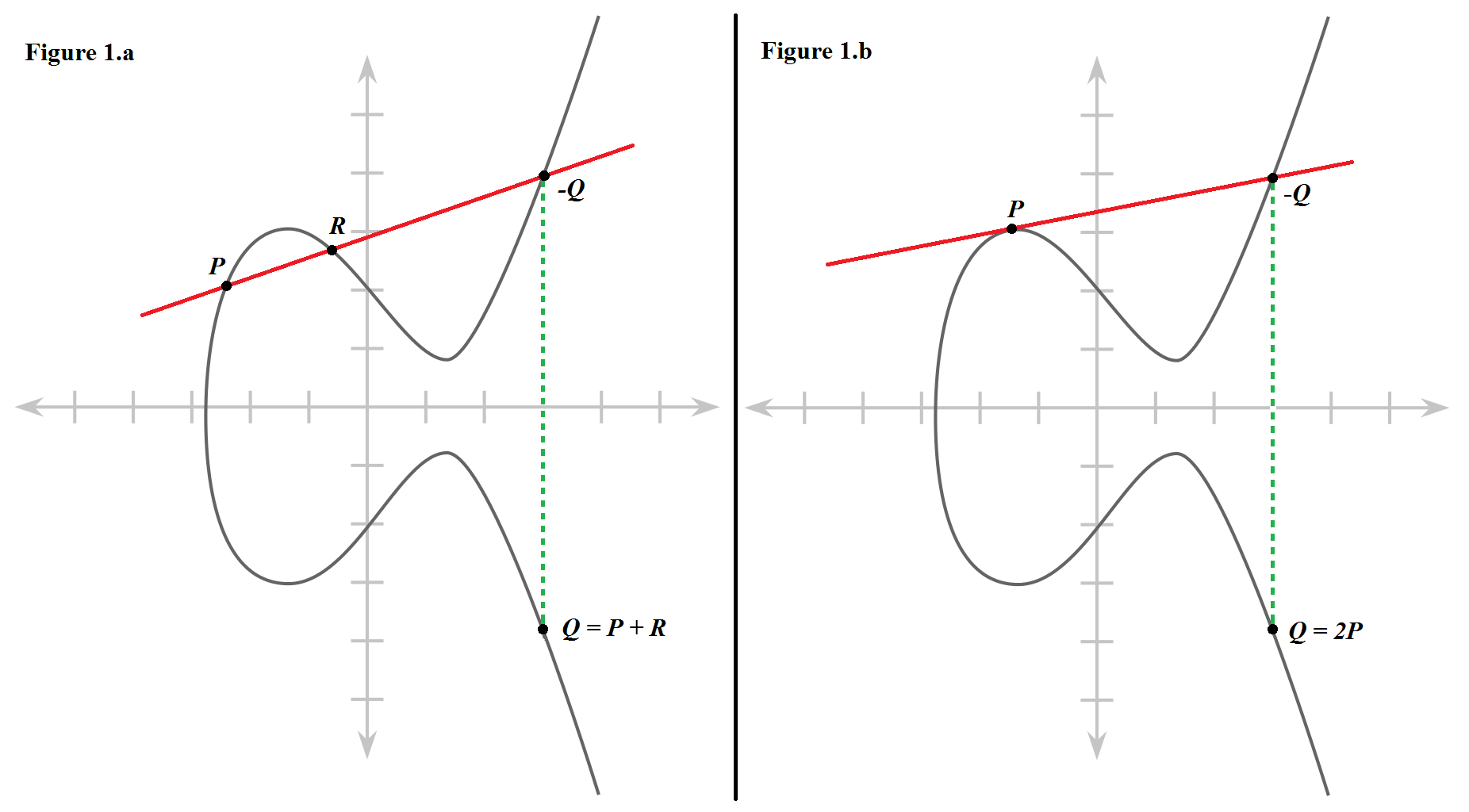
Pour définir l’addition Q = P + R, il faut tracer une droite reliant P et R. Cette droite (en rouge sur la figure 1.a) coupe la courbe elliptique en un troisième point appelé -Q (expliquer ce que représente ce point -Q est hors du contexte simplifié de cet article). Le symétrique de ce point par rapport à l’axe des abscisses (obtenu en suivant la droite pointillée verte sur la figure 1.a) est le résultat Q de cette addition.
Pour définir l’addition d’un point P avec lui-même, c’est-à-dire la multiplication de points pour k = 2, c’est-à-dire Q = P + P = 2P, il faut tracer la tangente à la courbe elliptique au point P. Cette droite (en rouge sur la figure 1.b) coupe la courbe elliptique en un point appelé -Q. Comme pour l’addition classique, le symétrique de ce point par rapport à l’axe des abscisses (obtenu en suivant la droite pointillée verte sur la figure 1.b) est le résultat Q de cette addition.
La cryptographie sur courbes elliptiques
Dans l’article précédent, nous avons expliqué que la sécurité de l’ECC repose sur l’ECDLP (Elliptic Curve Discrete Logarithm Problem en anglais), i.e. si l’on a un point P sur une courbe elliptique EC, alors :
- il est facile de calculer la multiplication de points Q = k*P pour un entier k quelconque,
- mais il est très difficile de retrouver la valeur de k quand on ne connait que P et Q.
En partant de cela, on peut donc construire un système de cryptographie à clé publique (Public-Key Cryptography en anglais, PKC), comme illustré surla figure ci-dessous, basé sur les courbes elliptiques. La clé privée d’Alice privKey est alors un entier kAlice et la clé publique correspondante pubKey est le point QAlice, résultat de l’opération kAlice * P où P est un point publiquement connu.
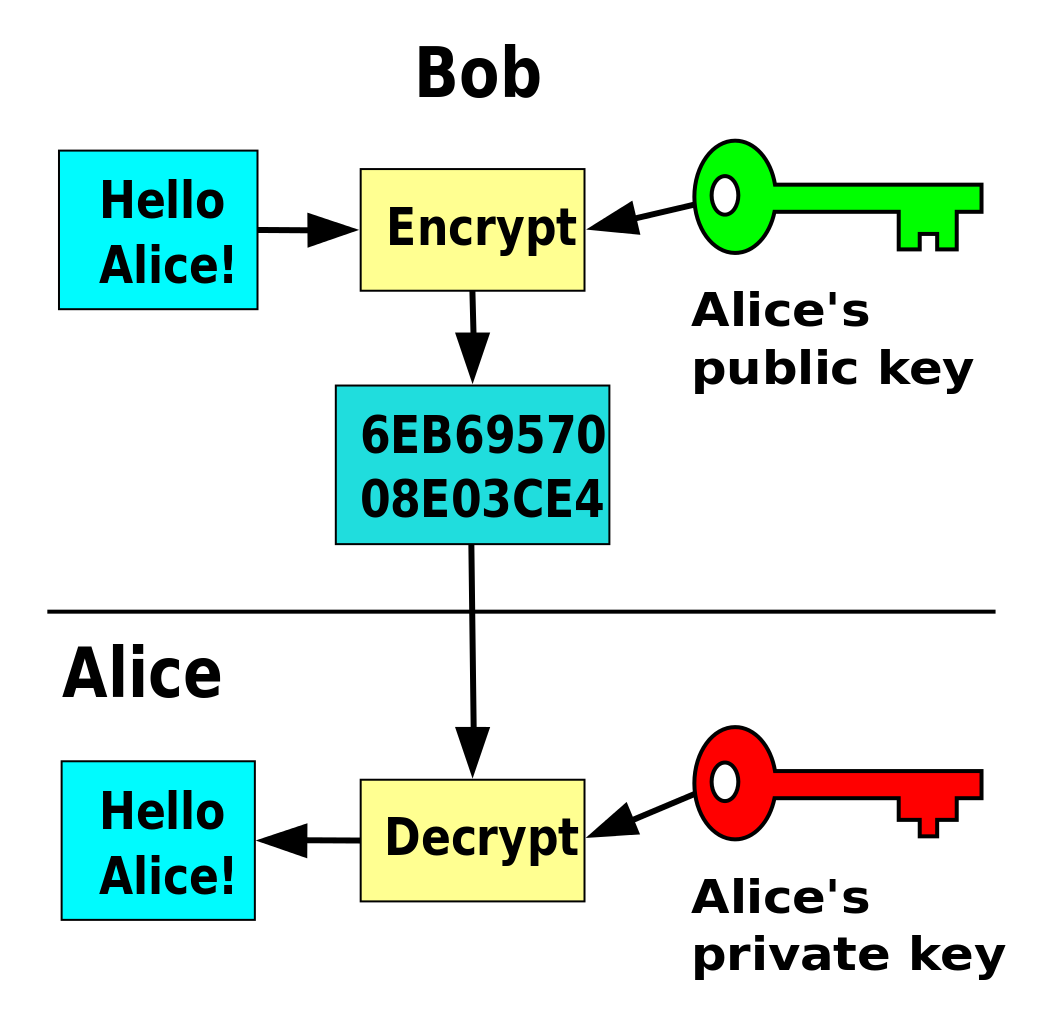
Schéma de chiffrement basé sur de la PKC. Bob chiffre le message qu’il souhaite envoyer à Alice avec sa clé publique (connue de tous), et Alice retrouve le message original en déchiffrant le message chiffré avec sa clé privée (connue d’elle seule).
(Image: By Tos (Own work) [Public domain], via Wikimedia Commons)
L’ECC est principalement utilisée pour le chiffrement de données, la signature digitale, la génération de nombres pseudo-aléatoires, et bien d’autres. Parmi les schémas cryptographiques les plus connus, on retrouve l’algorithme ECDSA (Elliptic Curve Digital Signature Algorithm) ou encore le protocole d’échanges de clés ECDH (Elliptic Curve Diffie-Hellman).
Un exemple concret : le protocole ECDH
Attardons nous un peu sur le protocole ECDH, car il est un exemple très pédagogique de l’utilisation des courbes elliptiques. En réalité, ce protocole est une variante du protocole de Diffie-Hellman (du nom de ses inventeurs), à l’origine basé sur le groupe multiplicatif des entiers modulo p, avec p étant un nombre premier. Le protocole original a été l’un des premiers exemples d’échange de clés dans le domaine de la cryptographie. Datant du milieu des années 70, le protocole de Diffie-Hellman permet à deux entités (Alice et Bob), qui ne se connaissent absolument pas, de se mettre d’accord sur un secret partagé, même en utilisant un canal de communication non sécurisé (i.e. qui peut être écouté par des personnes malveillantes). Le secret partagé peut ensuite être utilisé pour chiffrer la communication suivante entre Alice et Bob.
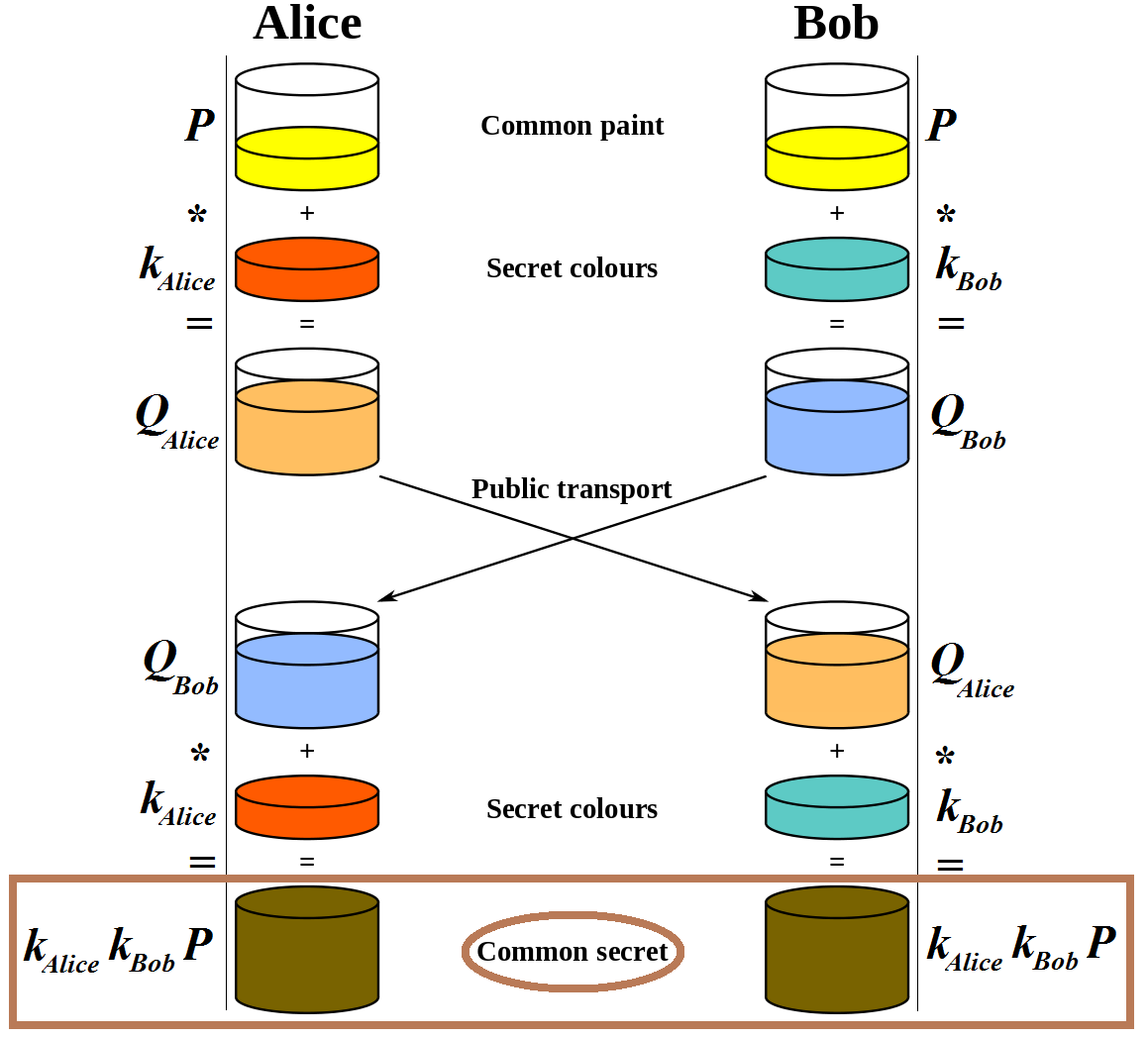
La figure ci-dessus illustre le principe du protocole ECDH. Tout d’abord, Alice et Bob connaissent un point P sur une courbe elliptique, P étant une donnée publique (la couleur jaune). Ensuite, chacun va choisir un secret : kAlice (en rouge) et kBob (en vert). A partir de là, chacun va calculer la valeur publique de son secret : QAlice = kAlice * P (en orange) et QBob = kBob * P (en bleu). Alice et Bob s’échangent ensuite leurs valeurs publiques. Ils peuvent même les divulguer publiquement : cela ne réduit pas la sécurité du protocole étant donné que la sécurité repose sur le problème ECDLP (cf. l’explication donnée dans notre précédent article). Enfin, Alice et Bob calculent le secret partagé (en marron) : kAlice * QBob pour Alice, et kBob * QAlice pour Bob. Ces deux calculs mènent au même secret partagé car :
kAlice * QBob = kAlice * (kBob * P) = kAlice * kBob * P = kBob * (kAlice * P) = kBob * QAlice.
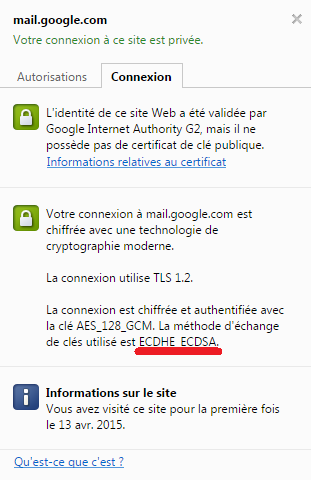
Un exemple concret (ci-contre) qui joint l’utilisation de ECDH et de ECDSA est le certificat SSL de certains sites web, tels que celui de Gmail. Notons que pour ce dernier, le protocole d’échange de clés est ECDHE, une variante de ECDH où les secrets choisis par les deux entités communicantes sont éphémères (d’où le “E” rajouté à l’accronyme), c’est-à-dire utilisés que temporairement, par exemple pour une seule session de communication. Ce choix permet ainsi de fournir une confidentialité persistante (forward secrecy en anglais) : même si un adversaire retrouve les secrets éphémères d’une session compromettant ainsi les communications correspondantes, il ne sera pas capable de compromettre les communications d’une session antérieure.
Les points négatifs de l’ECC
Ce n’est malheureusement pas tout rose dans le monde des courbes elliptiques. Plusieurs questions et doutes mis en avant ont énormément retenu les industriels de se lancer dans l’aventure ECC.
L’élément déclencheur a été l’histoire avec Dual_EC_DRBG (Dual Elliptic Curve Deterministic Random Bit Generator), algorithme qui génère des nombres aléatoires en se basant sur les mathématiques des courbes elliptiques. Le problème est que cet algorithme, standardisé par le NIST et promu par la NSA,ne semble pas être si aléatoire que cela. Il semblerait en effet que la séquence de nombres renvoyés par l’algorithme pourrait être complètement prédite par une personne connaissant certains paramètres secrets de la courbe elliptique (cf. ce post pour des détails plus techniques sur les vulnérabilités de Dual_EC_DRBG) : dans le jargon, c’est ce que l’on appelle une backdoor. Que cet algorithme ait été écrit spécifiquement avec cette backdoor ou pas ne change pas la puissance des mathématiques sur les courbes elliptiques ; cela soulève plutôt des questions sur les processus de standardisation des courbes elliptiques pour la cryptographie.
Cette histoire a créé une atmosphère de méfiance au sein de la communauté cryptographique vis-à-vis du NIST. Même si aucune nouvelle faille ou backdoor n’a été trouvée jusqu’à présent pour les courbes standardisées par le NIST, les cryptographes recommandent d’en utiliser d’autres, telles que celle de Dan Bernstein, ou encore celles de Paulo Baretto et al. Malheureusement, ces courbes elliptiques non-conventionnelles vont mettre beaucoup de temps à être acceptées et utilisées à grande échelle.
Que retenir de l’ECC?
La cryptographie sur courbes elliptiques est l’une des plus puissantes techniques dans le domaine. Grâce à ses petites longueurs de clés, leur stockage peut se faire dans des environnements limités (p.ex. les tags RFID des passeports biométriques) et les calculs sont exécutés plus rapidement qu’avec de la cryptographie classique telle que RSA, tout en assurant un haut niveau de sécurité. L’ECC se montre donc très prometteuse pour le futur, malgré les doutes soulevés par la communauté cryptographique vis-à-vis des recommandations et standards du NIST à son sujet.

Leave a Reply