La cryptographie sur courbes elliptiques, ou Elliptic Curve Cryptography (ECC) en anglais, est un des plus puissants types de cryptographie utilisée aujourd’hui. On retrouve cette technologie dans de nombreux exemples du quotidien, tels que dans le protocole HTTPS d’un grand nombre de sites web ou dans certaines cartes d’identité (p.ex. pour la méthode de signature digitale des eID allemandes et autrichiennes). Bien que puissante, force est de constater que l’ECC est malgré tout un des types de cryptographie les moins compris, essentiellement car elle est basée sur une somme de notions mathématiques complexes. Or il nous semble important que chaque personne puisse comprendre, même dans les grandes lignes, la technologie qui se cache derrière les systèmes sécurisés auxquels elle fait confiance.

C’est pourquoi je vais me lancer dans une série de blogs qui vont vous présenter petit à petit l’ECC et les courbes elliptiques, tout en essayant de simplifier au maximum leurs mathématiques fondatrices complexes. Je remercie par avance les experts dans le domaine qui comprendront qu’il n’est pas possible de rentrer dans les détails lorsqu’on souhaite présenter l’ECC aux non-initiés.

ECC, c’est quoi?

L’ECC est une approche de la cryptographie à clé publique (Public-Key Cryptography en anglais, PKC), où il est requis d’avoir deux clés bien séparées: une clé privKey dite “privée” et une autre clé pubKey dite “publique”. La figure ci-dessous explique comment ces deux clés peuvent être utilisées dans un schéma standard de PKC quand Bob souhaite envoyer un message chiffré à Alice.

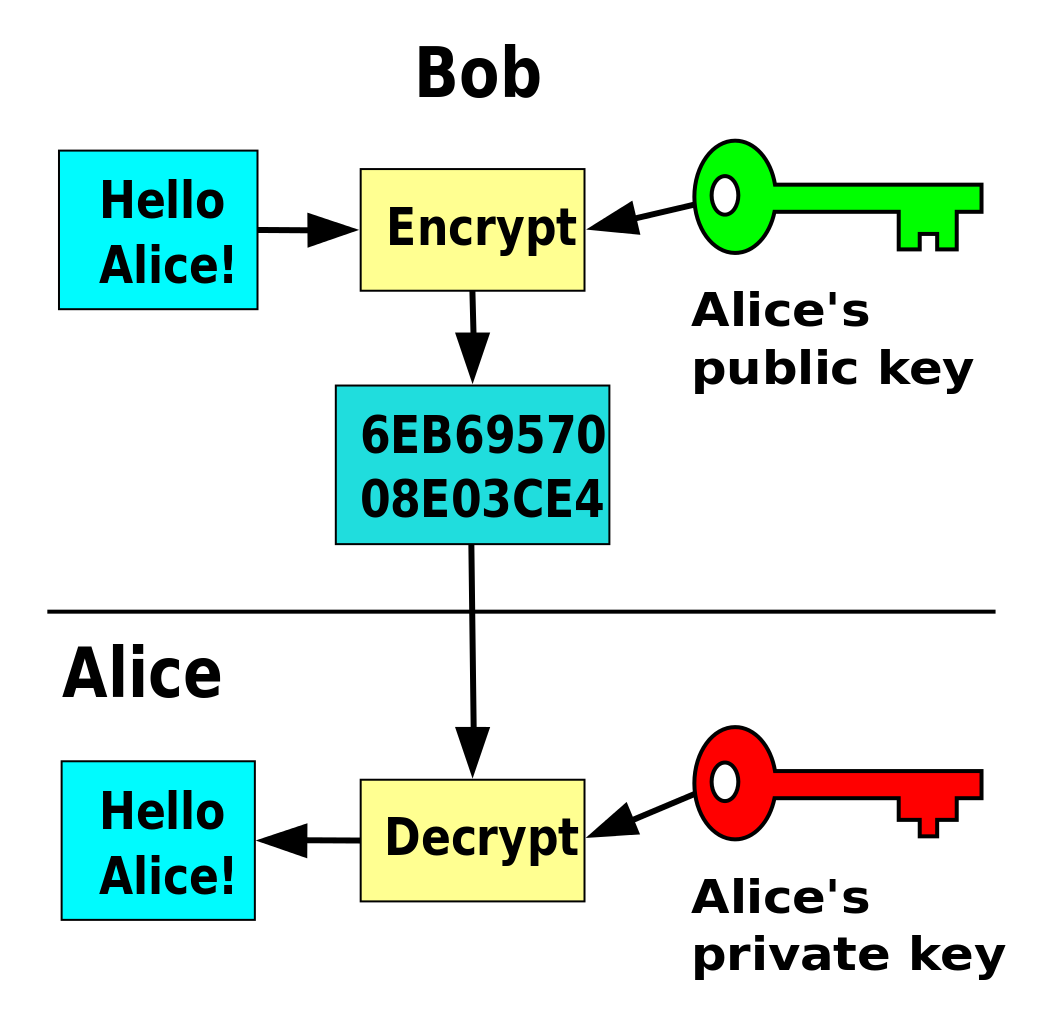
Schéma de chiffrement basé sur de la PKC. Bob chiffre le message qu’il souhaite envoyer à Alice avec sa clé publique (connue de tous), et Alice retrouve le message original en déchiffrant le message chiffré avec sa clé privée (connue d’elle seule).
(Image: By Tos (Own work) [Public domain], via Wikimedia Commons)

L’utilisation des courbes elliptiques pour la cryptographie a été introduite indépendamment par Neal Koblitz et Victor S. Miller en 1985. Ces deux chercheurs ont vu le potentiel offert par la structure mathématique des courbes elliptiques — intensément étudiées dans la théorie des nombres depuis plus de 100 ans — pour l’adapter à la cryptographie. A la fin des années 1990, l’ECC a été standardisée par un certain nombre d’organisations (p.ex. ANSI X9.63, IEEE P1363, ISO 15946, NIST SP 800-56), et elle a commencé à être acceptée pour commercialisation. De nos jours, l’ECC est principalement utilisée dans les environnements à faible ressource tels que les réseaux sans fil ad-hoc et les réseaux mobiles, car elle ne nécessite pas de longues clés cryptographiques pour assurer un haut niveau de sécurité.

Pour être plus précis sur ce dernier point, un des problèmes majeurs des systèmes conventionnels basés sur la PKC est que la longueur des clés doit être suffisamment grande pour assurer un niveau de sécurité élevé. Ceci se traduit par une faible vitesse et une grande consommation de la bande passante. C’est là que la force de l’ECC rentre en jeu : comme l’a établit le NIST, là où le système cryptographique bien connu RSA a besoin de clés de 1024 bits, l’ECC n’a besoin que de clés de 160 bits pour atteindre le même niveau de sécurité.

A quoi ressemble une courbe elliptique ?

Contrairement à ce que l’on pourrait croire, une courbe elliptique n’est pas une ellipse. Historiquement, le terme “courbe elliptique” vient en réalité de l’association de ces courbes avec les intégrales elliptiques, ces dernières servant à calculer la longueur des arcs d’une ellipse.

Pour son utilisation en cryptographie, une courbe elliptique est définie sur un corps fini K, c’est-à-dire sur un ensemble fini d’éléments avec lesquels on est capable de faire des additions, soustractions, multiplications et divisions. Par exemple, le corps fini K le plus connu est l’ensemble {0,1} des booléens (dont les calculs sont faits sur un seul bit d’information). L’équation la plus simplifiée d’une courbe elliptique est de la forme

y² = x³ + ax + b

où a et b sont les coefficients de la courbe et appartiennent à K. La figure ci-dessous illustre les différentes représentations graphiques d’une courbe elliptique avec son équation simplifiée, dépendamment des valeurs de a et de b.

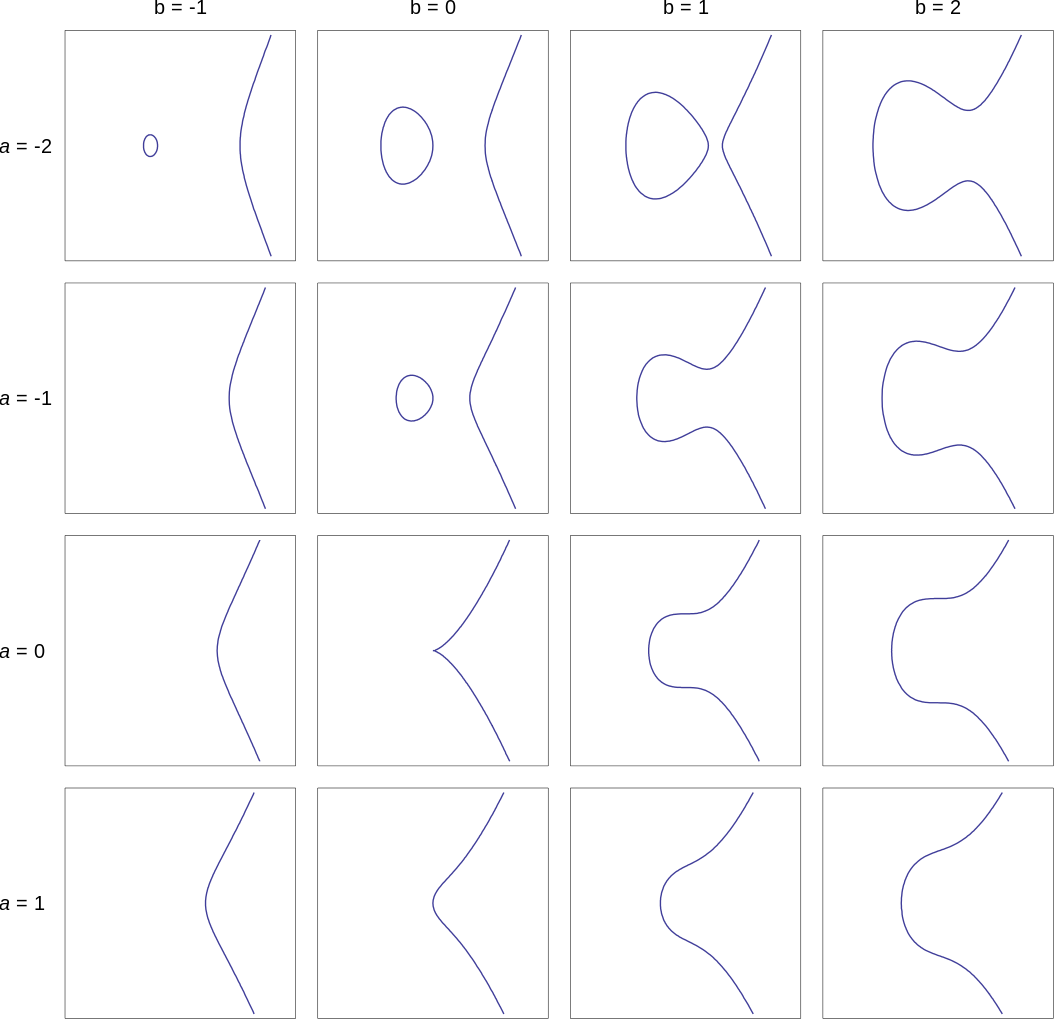
Quelques exemples de courbes elliptiques. Notez que pour a=0 et b=0, la courbe n’est pas “régulière” et donc n’est pas considérée comme une courbe elliptique.
(Image: Tos (Own work) [Public domain], via Wikimedia Commons)

Mathématiquement parlant, une courbe elliptique est un groupe avec des caractéristiques particulières. Pour simplifier, une courbe elliptique est un ensemble d’éléments — les points de la courbe — avec lesquels on peut effectuer des opérations mathématiques bien précises :

• L’addition de points : quand on a deux points P et R sur une courbe elliptique EC, alors on peut calculer leur addition Q = P + R, et le résultat Q appartient aussi à EC.
• La multiplication de points : quand on a un point P sur une courbe elliptique EC, alors on peut additionner k fois ce même point (p.ex. si k = 2, alors on peut calculer P + P), ce qui résulte en la multiplication de points Q = k*P (p.ex. si k = 2, alors Q = 2*P = P + P), et le résultat Q appartient aussi à EC.

Nous verrons plus tard comment s’effectuent ces opérations mathématiques. Mais finalement, ce qu’il faut retenir, c’est qu’on peut faire des opérations sur les points d’une courbe elliptique, de la même façon qu’on peut faire 1 + 2 = 3 ou encore 3 + 3 = 2*3 quand on fait des calculs avec des nombres réels.

ECDLP, le fondement de la sécurité de l’ECC

Les systèmes cryptographiques modernes utilisés en PKC sont généralement basés sur des problèmes mathématiques dits “durs”, ou “computationally infeasible” en anglais, c’est-à-dire qui n’admettent aucune solution efficace pour résoudre le problème. Par exemple, la sécurité de RSA repose sur le problème de la factorisation entière en nombres premiers : il est facile d’obtenir le produit de deux grands nombres premiers, par contre il est beaucoup plus difficile de trouver les facteurs premiers de celui-ci. Pour visualiser la difficulté du problème, prenons un premier exemple où le produit à factoriser est 91 : on peut facilement retrouver que 91 = 7*13 car ce sont de petits nombres. Maintenant, si nous prenons le nombre appelé RSA-1024 ci-dessous comme deuxième exemple, alors personne à l’heure actuelle n’a été capable de retrouver ses deux facteurs premiers. Jusqu’en 2007, la compagnie RSA Security offrait d’ailleurs 100 000 $ à la première personne réussissant l’exploit.

RSA-1024 = 135066410865995223349603216278805969938881475605667027524485143851526510604859533833940287150571909441798207282164471551373680419703964191743046496589274256239341020864383202110372958725762358509643110564073501508187510676594629205563685529475213500852879416377328533906109750544334999811150056977236890927563

Pour les systèmes cryptographiques basés sur l’ECC, leur sécurité repose sur le problème du logarithme discret dans un groupe mathématique défini par une courbe elliptique, appelé Elliptic Curve Discrete Logarithm Problem (ECDLP) en anglais. Pour comprendre ce que cela veut dire, expliquons ce problème étape par étape. Tout d’abord, le simple DLP signifie que, si l’on a un élément g d’un groupe mathématique G, alors on peut facilement calculer la valeur b = g^k  pour un entier k quelconque. Mais il est très difficile de retrouver la valeur de k quand on ne connait que b et g. Bien sûr, la difficulté est réelle quand b, g, k sont de très grands nombres, comme pour la factorisation expliquée au paragraphe précédent. L’ECDLP reprend le même problème que le simple DLP en considérant que, si l’on a un point P sur une courbe elliptique EC, alors :

• il est facile de calculer la multiplication de points Q = k*P pour un entier k quelconque,
• mais il est très difficile de retrouver la valeur de k quand on ne connait que P et Q.

To be continued…

Dans un prochain blog, nous expliquerons “graphiquement” les opérations mathématiques qui peuvent s’effectuer sur une courbe elliptique (i.e. l’addition et la multiplication de points). Nous verrons également comment se servir des courbes elliptiques pour faire de la cryptographie. Comment sont choisies et calculées les clés privKey et pubKey ? Quels sont les systèmes cryptographiques les plus connus se basant sur l’ECC et comment fonctionnent-ils?