Dans notre article précédent, nous avons montré comment il était possible de calculer la zone accessible dans un délai donné à partir d’un ensemble de points de départ (ou d’arrivée), comme une maternité, un départ SMUR ou un centre de vaccination Covid.
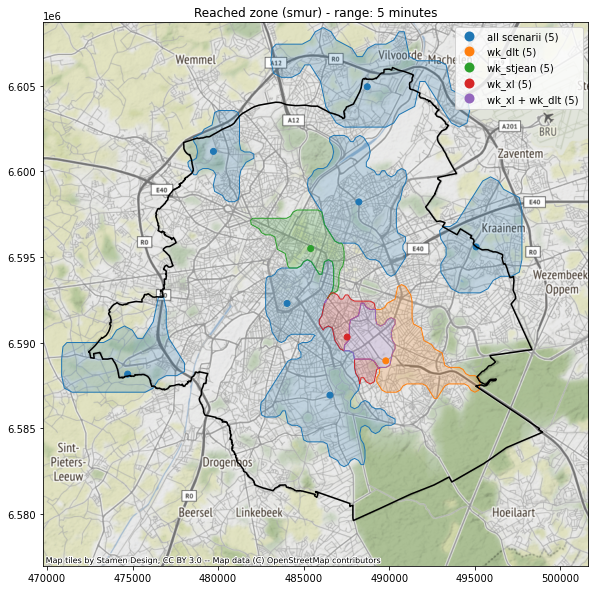
Les cartes présentées ont le grand avantage de donner une très bonne vue d’ensemble sur les zones accessibles ou non en fonction des scénarios, mais elles présentent l’inconvénient qu’il est malaisé de comparer deux scénarios dans leur globalité. Par ailleurs, la population n’est pas uniformément répartie, et ce n’est pas parce qu’une configuration couvre une plus grande superficie qu’une autre qu’elle est plus intéressante pour la majorité des citoyens.
Dans cet article, nous présenterons deux types de graphiques permettant de comparer objectivement deux scénarios (sous les hypothèses simplificatrices présentées dans notre article précédent). Le premier s’intéressera à la couverture territoriale, le second à la couverture populationnelle.
Couverture territoriale
Dans les trois use cases présentés dans notre article précédent, nous nous intéressions à un territoire précis : la région de Bruxelles-Capitale pour les cas “SMUR” et “Vaccin Covid”, et la Belgique dans son ensemble pour le cas “Maternité”. Nous aimerions pouvoir nous poser les questions typiques suivantes : Quelle proportion du territoire cible a accès à un centre de vaccination en 10 minutes ? Cette proportion augmenterait-elle si l’on avait ouvert un centre supplémentaire dans le sud-est de Bruxelles ? Dans les trois semaines en alternance des départs SMUR, est-ce qu’une d’entre elles se démarque en termes d’accessibilité ?
Le graphique (interactif) ci-dessous présente le use case “SMUR” à Bruxelles. Chacun des trois scénarios est représenté par une courbe. L’axe horizontal représente le temps de parcours, l’axe vertical la proportion de territoire couvert sur ce délai par (au moins) un des départs SMUR ouvert dans le scénario concerné. Cette proportion correspond au ratio entre la superficie du multi-polygone accessible dans un délai et un scénario donné et la superficie du territoire analysé.
On observe que les scénarios “Saint-Jean” et “Ixelles” sont à peine différentiables, quel que soit le délai. Cela ne signifie pas nécessairement que le même territoire est atteint, simplement que quasiment la même superficie l’est. Il se peut très bien par exemple qu’un quartier soit accessible en 5 minutes uniquement la semaine d’Ixelles, mais une autre zone de grosso-modo la même superficie sera alors uniquement accessible en 5 minutes la semaine de Saint-Jean.
On remarque par contre que quel que soit le délai, le territoire atteint la semaine de Delta est plus important que les deux autres semaines. Et la totalité du territoire est atteignable en 12 minutes les semaines de Delta, pour 15 minutes les autres (moyennant un facteur multiplicatif défini dans l’article précédent).
L’écart entre les courbes est cependant relativement faible, surtout si on le compare au cas des centres de vaccination ci-dessous. Celui-ci nous indique que personne ne doit rouler plus de 16 minutes pour arriver dans un centre de vaccination ; si le centre de Watermael-Boitsfort avait ouvert, ce délai serait tombé à 12.
Le graphique dans le cas des maternités nous montre qu’en 30 minutes de temps de parcours, 96.4 % du territoire est atteignable avec la situation actuelle, contre 95.9 % avec les fermetures attendues. En 35 minutes, le ratio monte à 99 (vs 98.8) %.
Couverture populationnelle
Une future maman sur le point d’accoucher a peu de chance de se retrouver en plein milieu d’une vaste étendue de forêt au moment où elle doit se rendre à la maternité. Ouvrir un centre de vaccination au beau milieu de la forêt de Soignes (au sud-est de Bruxelles) permettrait sans doute d’augmenter la couverture territoriale dans un délai donné, mais n’aurait pas beaucoup de sens d’un point de vue économique et organisationnel. Au lieu de se demander quel est le territoire que peut atteindre un SMUR dans un délai donné, on peut aussi se demander quelle proportion de la population peut être atteinte dans ce délai.
Nous avons à notre disposition sur https://statbel.fgov.be la liste de tous les “secteurs statistiques“, qui découpent la Belgique en près de 20.000 secteurs, allant de moins de 3 hectares à près de 150 km². Pour chacun de ces secteurs, nous connaissons les frontières, ainsi que la population qui y est domiciliée (certains secteurs sont inhabités, d’autres hébergent jusqu’à 8.300 personnes).
Notons que nous ne considérons ici que le lieu de domicile. Or en journée la semaine, une majorité de la population se trouve sur son lieu de travail (quand le télétravail n’est pas la norme). Notre analyse pourrait être affinée si nous utilisions, par exemple, les données collectées par les opérateurs de téléphonie mobile à propos des mouvements de population.
Jointure spatiale
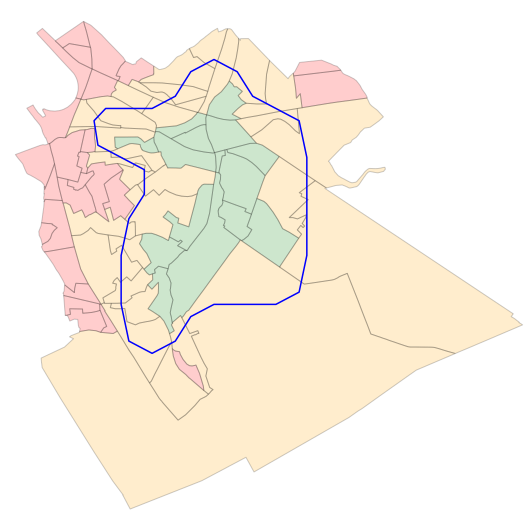
Pour connaitre la population pouvant être atteinte à partir d’un ensemble de points dans un délai donné, nous pouvons réaliser une jointure spatiale (cf. notre article à ce sujet) entre le (multi-)polygone décrivant le territoire atteignable dans le délai donné (courbe bleue dans l’image ci-dessous), et l’ensemble des secteurs statistiques. Il suffira ensuite de sommer les populations de tous les secteurs statistiques faisant partie de la jointure. Bien sûr, les frontières de l’un ne correspondront pas aux frontières de l’autre, comme l’illustre la figue ci-dessous.
Il existe plusieurs types de jointure spatiale. La plus restrictive (de type ‘contains‘) consiste à n’inclure dans la jointure que les polygones de l’ensemble de droite (les secteurs statistiques) qui sont strictement inclus dans l’ensemble de gauche (la courbe isochrone, en bleu), représentés en vert dans la figure.
La moins restrictive (type ‘intersect’) inclut dans la jointure tous les secteurs statistiques ayant une partie de la surface en commun avec le polygone défini par la courbe isochrone, et inclut donc les secteurs verts et oranges.
On sait que l’ensemble de la population des secteurs verts est bien incluse dans la courbe bleue. Les secteurs (en orange) qui sont traversés par la courbe isochrone sont plus difficiles à appréhender. L’hypothèse la plus pessimiste (‘contains‘) consiste à considérer que toute la population de ces secteurs habite en fait dans la partie du secteur à l’extérieur de la courbe bleue. Dans ce cas, on ne considère que la population des secteurs verts. L’hypothèse la plus optimiste (‘intersects’) consiste à considérer l’inverse : les habitants sont tous “du bon côté de la courbe”. Dans cette hypothèse, on rajoutera les secteurs orange dans leur intégralité.
Une hypothèse intermédiaire consiste à supposer que la population est uniformément répartie dans chaque secteur. Si la courbe bleue intègre 25 % d’un secteur, on suppose alors que 25 % de sa population est couverte.
Dans le graphique ci-dessous, les courbes “solides” reprennent cette hypothèse moyenne intermédiaire. Chacune d’elle est entourée d’une bande d’incertitude qui va de l’hypothèse la plus optimiste (“UB”, pour “upper bound”, quand on place le curseur sur la courbe) à la plus pessimiste (LB).
On peut y faire deux constats qui ont probablement la même explication :
- En dix minutes, on peut atteindre 83.8 (St-Jean) à 88.2 % (Delta) du territoire, mais 94.8 (St-Jean) à 96.5 % (Delta) de la population, selon l’hypothèse moyenne
- La différence entre les 3 scénarios est nettement moins marquée en termes de territoire qu’en termes de population.
Nous supposons que cela s’explique par le fait que le départ de Delta rend en grande partie plus accessible… la forêt de Soignes, quasiment inhabitée, mais qui recouvre 10 % du territoire de Bruxelles-Capitale.
Selon les hypothèses simplificatrices présentées précédemment, la proportion qui perdra la possibilité d’accès à une maternité en 30 minutes est faible (0.01%, soit de 99.72 % à 99.71 % ; 0.07% en cas de trafic), largement inférieure à la précision que peut offrir cette analyse. Cela ne veut bien sûr pas dire que la fermeture n’aura pas d’impact : entre 5 et 25 minutes de parcours, de 4 à 5 % de la population voit son temps de trajet augmenter.
Autres cas d’usages
Nous avons focalisé notre analyse sur la comparaison de scénarios. Mais une légère variante de notre analyse permettra, par exemple, de déterminer la proportion de la population qui a accès à une infrastructure (bureau de poste, gare, CPAS, cabinet médical…) en fonction du temps de parcours. On pourrait ainsi comparer plusieurs provinces (au lieu de scénario), pour mieux évaluer les provinces qui nécessitent le plus d’investissement. Ou voir dans quelle région il serait bon de recruter un contrôleur “de terrain” (fiscal, social,…) pour minimiser les temps de parcours, en fonction de sa population cible.
Conclusions
Nous insistons à nouveau : les chiffres présentés ci-dessus ne sont pas suffisants pour valider ou contester les choix pris par les décideurs. Ils ne sont qu’un élément parmi bien d’autres. Les conséquences de la fermeture ou de la non-ouverture d’une infrastructure vont bien au-delà du temps de parcours : conséquences sociales, économiques, politiques, environnementales…
Mais cette présentation montre que mesurer l’impact d’une décision avec une composante géographique peut s’avérer un problème complexe, qui ne peut pas être résolu en quelques schémas ou formules dans un fichier Excel. La plus-value du data scientist est devenue aujourd’hui incontestable pour éclairer les choix pris par nos décideurs.
Ce post est une contribution individuelle de Vandy Berten, spécialisé en data science chez Smals Research. Cet article est écrit en son nom propre et n’impacte en rien le point de vue de Smals.

Leave a Reply